其他优化

有效前沿方法涉及受约束的目标的直接优化。 然而，有一些投资组合优化方案在性质上是完全不同的。 PyPortfolioOpt 提供了对这些替代方案的支持，同时仍然让你可以使用相同的前处理和后期处理 API。

备注

从 v0.4 开始，这些其他的优化器现在都继承自 BaseOptimizer 或 BaseConvexOptimizer ，所以你不再需要自己实现预处理和后期处理方法。 因此，你可以轻松地将 EfficientFrontier 换成 HRPOpt 。

分层风险平价 (HRP)

层次风险平价是 Marcos Lopez de Prado [1] 开发的一种新的投资组合优化方法。 详细的解释可以在链接的论文中找到，这里是HRP工作原理的一个粗略概述：

1. 从一整批资产中，根据资产的相关性形成一个距离矩阵。

2. 利用距离矩阵，通过分层聚类将资产聚成一棵树。

3. 在树的每个分支中，形成最小方差的投资组合（通常只在两个资产之间）。

4. 遍历每一层，在每个节点上优化组合小型投资组合。

这样做的好处是，它不需要像传统的均值-方差优化那样对协方差矩阵进行反转，而且似乎可以产生多样化的组合，在样本外表现良好。

hierarchical_portfolio 模块旨在实现投资组合优化的最新进展之一分层聚类模型应用于分配。

所有的分层类都有类似于 EfficientFrontier 的 API，不过由于目前很多分层模型不支持不同的目标，所以实际的分配是通过调用 optimize() 来实现的。

目前已经实现：

• HRPOpt 实现了分层风险平价（HRP）组合。代码由 Marcos Lopez de Prado (2016) 许可转载。

class pypfopt.hierarchical_portfolio.HRPOpt(returns=None, cov_matrix=None)

HRPOpt 对象（继承自 BaseOptimizer）构建了一个分层风险平价投资组合。

可用变量:

• 输入

  • n_assets - int

  • tickers - str list

  • returns - pd.DataFrame

• 输出:

  • weights - np.ndarray

  • clusters - linkage matrix corresponding to clustered assets.

公共方法:

• optimize() 使用 HRP 计算权重

• portfolio_performance() 计算优化后投资组合的期望收益率、波动率和夏普比率。

• set_weights() 从权重数据中创建 self.weights (np.ndarray)。

• clean_weights() 对权重进行四舍五入，并剪掉接近零的部分。

• save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(returns=None, cov_matrix=None)

参数:

• returns (pd.DataFrame) – asset historical returns

• cov_matrix (pd.DataFrame.) – covariance of asset returns

抛出:

TypeError – if returns is not a dataframe

optimize(linkage_method='single')

使用 Scipy 分层聚类法，构建一个分层风险平价投资组合（见 这里 ）

参数:

linkage_method (str) – which scipy linkage method to use

返回:

weights for the HRP portfolio

返回类型:

OrderedDict

portfolio_performance(verbose=False, risk_free_rate=0.02, frequency=252)

优化后，计算（并可选择打印）最优投资组合的表现。目前计算的是期望收益率、波动率和夏普比率，假设收益率是日频的。

参数:

• verbose (bool, optional) – whether performance should be printed, defaults to False

• risk_free_rate (float, optional) – risk-free rate of borrowing/lending, defaults to 0.02. The period of the risk-free rate should correspond to the frequency of expected returns.

• frequency (int, optional) – number of time periods in a year, defaults to 252 (the number of trading days in a year)

抛出:

ValueError – if weights have not been calculated yet

返回:

expected return, volatility, Sharpe ratio.

返回类型:

(float, float, float)

临界线算法

这是一个二次求解器稳健的替代方法，用于寻找均值方差最优投资组合，当我们应用线性不等式时，它尤其具有优势。 与一般的凸优化程序不同，CLA 是专门为投资组合优化设计的。它保证在一定数量的迭代后收敛，并能有效地得出整个有效边界。

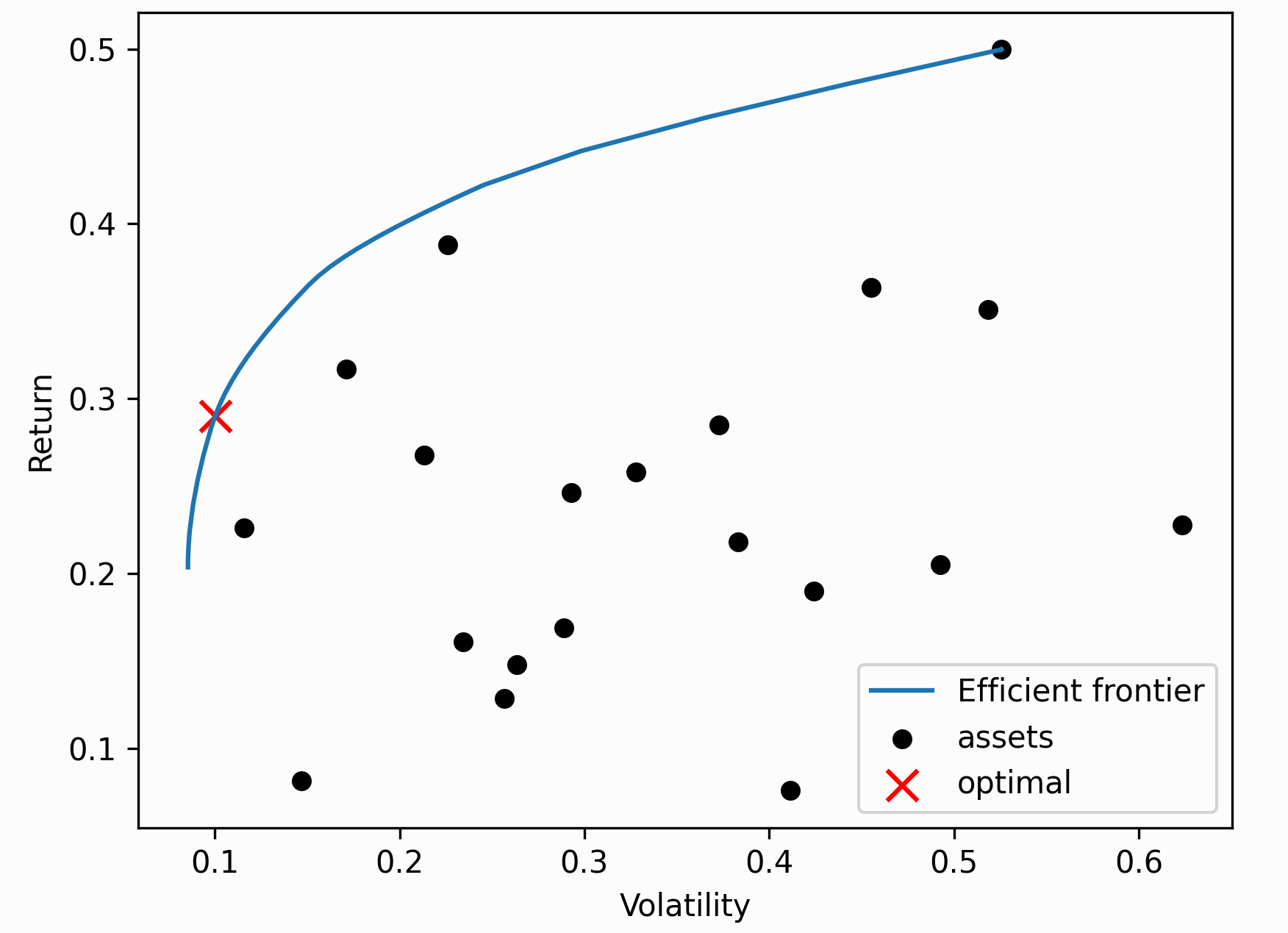
小技巧

一般来说，我会选择标准的 EfficientFrontier 优化器，除非有特殊的要求，比如想有效地计算整个有效边界来进行绘图。

非常感谢 Marcos López de Prado 和 David Bailey 完成的功能 [2] 。 我们已经通过电子邮件收到了对其分发的许可。 我们对它进行了修改，使其具有相同的 API，尽管从 v0.5.0 开始我们只支持 max_sharpe() 和 min_volatility() 。

cla 模块包含 CLA 类，它使用 Marcos Lopez de Prado 和 David Bailey 完成的临界线算法生成最佳投资组合。

class pypfopt.cla.CLA(expected_returns, cov_matrix, weight_bounds=(0, 1))

可用变量:

• 输入:

  • n_assets - int

  • tickers - str list

  • mean - np.ndarray

  • cov_matrix - np.ndarray

  • expected_returns - np.ndarray

  • lb - np.ndarray

  • ub - np.ndarray

• 优化参数:

  • w - np.ndarray list

  • ls - float list

  • g - float list

  • f - float list list

• 输出:

  • weights - np.ndarray

  • frontier_values - (float list, float list, np.ndarray list)

公共方法:

• max_sharpe() 优化最大夏普比率（又称切线组合）。

• min_volatility() 优化最小波动率

• efficient_frontier() 计算整个有效前沿。

• portfolio_performance() 计算优化后投资组合的期望收益率、波动率和夏普比率。

• clean_weights() 对权重进行四舍五入，并将接近零值的部分删除。

• save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(expected_returns, cov_matrix, weight_bounds=(0, 1))

参数:

• expected_returns (pd.Series, list, np.ndarray) – expected returns for each asset. Set to None if optimising for volatility only.

• cov_matrix (pd.DataFrame or np.array) – covariance of returns for each asset

• weight_bounds (tuple (float, float) or (list/ndarray, list/ndarray) or list(tuple(float, float))) – minimum and maximum weight of an asset, defaults to (0, 1). Must be changed to (-1, 1) for portfolios with shorting.

抛出:

• TypeError – if expected_returns is not a series, list or array

• TypeError – if cov_matrix is not a dataframe or array

efficient_frontier(points=100)

计算整个有效前沿。

参数:

points (int, optional) – rough number of points to evaluate, defaults to 100

抛出:

ValueError – if weights have not been computed

返回:

return list, std list, weight list

返回类型:

(float list, float list, np.ndarray list)

max_sharpe()

最大化夏普比率。

返回:

asset weights for the max-sharpe portfolio

返回类型:

OrderedDict

min_volatility()

最小化波动率。

返回:

asset weights for the volatility-minimising portfolio

返回类型:

OrderedDict

portfolio_performance(verbose=False, risk_free_rate=0.02)

优化后，计算（并可选择打印）最优投资组合的表现。目前计算的是期望收益率、波动率和夏普比率。

参数:

• verbose (bool, optional) – whether performance should be printed, defaults to False

• risk_free_rate (float, optional) – risk-free rate of borrowing/lending, defaults to 0.02

抛出:

ValueError – if weights have not been calculated yet

返回:

expected return, volatility, Sharpe ratio.

返回类型:

(float, float, float)

set_weights(_)

设置用户输入的权重属性（np.array）的实用函数

参数:

input_weights (dict) – {ticker: weight} dict

实现自己的优化器

请注意，这与实现 定制优化问题 是完全不同的，因为在这种情况下，我们仍然在使用相同的凸优化结构。 然而，HRP 和 CLA 优化有一个根本不同的优化方法。一般来说，与自定义目标函数相比，这些都是更难编码的。

要实现一个与 PyPortfolioOpt 其他部分兼容的自定义优化器，只需扩展 BaseOptimizer （或者 BaseConvexOptimizer ，如果你想使用 cvxpy 的话），这两者都可以在 base_optimizer.py 中找到。 这样你就可以访问像 clean_weights() 这样的实用方法，以及确保任何输出与 portfolio_performance() 和后期处理方法兼容。

base_optimizer 模块包含了父类 BaseOptimizer ，所有的优化器都将继承于此。 BaseConvexOptimizer 是所有 cvxpy （和 scipy ）优化的基类。

此外，我们定义了一个通用的效用函数 portfolio_performance 来评估一组给定的投资组合权重的收益和风险。

class pypfopt.base_optimizer.BaseOptimizer(n_assets, tickers=None)

可用变量:

• n_assets - int

• tickers - str list

• weights - np.ndarray

公共方法:

• set_weights() 从一个权重数据中创建 self.weights (np.ndarray)。

• clean_weights() 对权重进行四舍五入，并将接近零的部分剪掉。

• save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(n_assets, tickers=None)

参数:

• n_assets (int) – number of assets

• tickers (list) – name of assets

clean_weights(cutoff=0.0001, rounding=5)

帮助方法来清理原始权重，将绝对值低于分界线的权重设置为零，并对其余部分进行舍入。

参数:

• cutoff (float, optional) – the lower bound, defaults to 1e-4

• rounding (int, optional) – number of decimal places to round the weights, defaults to 5. Set to None if rounding is not desired.

返回:

asset weights

返回类型:

OrderedDict

save_weights_to_file(filename='weights.csv')

保存权重到一个文本文件的实用方法。

参数:

filename (str) – name of file. Should be csv, json, or txt.

set_weights(input_weights)

设置用户输入的权重属性（np.array）的实用函数

参数:

input_weights (dict) – {ticker: weight} dict

class pypfopt.base_optimizer.BaseConvexOptimizer(n_assets, tickers=None, weight_bounds=(0, 1), solver=None, verbose=False, solver_options=None)

BaseConvexOptimizer 包含许多私有变量供 cvxpy 使用。 例如，权重的不可变的优化变量被存储为 self._w。我们不鼓励直接与这些变量进行交互。

可用变量:

• n_assets - int

• tickers - str list

• weights - np.ndarray

• _opt - cp.Problem

• _solver - str

• _solver_options - {str: str} dict

公共方法:

• add_objective() 为优化问题添加一个（凸）目标。

• add_constraint() 在优化问题中加入一个约束条件。

• convex_objective() 解决一个带有线性约束的一般凸目标。

• nonconvex_objective() 使用 scipy 后端求解一个通用的非凸目标。这很容易陷入局部最小值，所以通常不推荐。

• set_weights() 从一个权重字典中创建 self.weights (np.ndarray)。

• clean_weights() 对权重进行四舍五入，并剪掉接近零的部分。

• save_weights_to_file() 将权重保存为 csv、json 或 txt。

__init__(n_assets, tickers=None, weight_bounds=(0, 1), solver=None, verbose=False, solver_options=None)

参数:

• weight_bounds (tuple OR tuple list, optional) – minimum and maximum weight of each asset OR single min/max pair if all identical, defaults to (0, 1). Must be changed to (-1, 1) for portfolios with shorting.

• solver (str, optional.) – name of solver. list available solvers with: cvxpy.installed_solvers()

• verbose (bool, optional) – whether performance and debugging info should be printed, defaults to False

• solver_options (dict, optional) – parameters for the given solver

_map_bounds_to_constraints(test_bounds)

将输入边界转换为 cvxpy 可以接受的形式，并添加到约束列表中。

参数:

test_bounds (tuple OR list/tuple of tuples OR pair of np arrays) – minimum and maximum weight of each asset OR single min/max pair if all identical OR pair of arrays corresponding to lower/upper bounds. defaults to (0, 1).

抛出:

TypeError – if test_bounds is not of the right type

返回:

bounds suitable for cvxpy

返回类型:

tuple pair of np.ndarray

_solve_cvxpy_opt_problem()

定义了目标和约束条件后，用辅助方法来解决 cvxpy 问题并检查输出。

抛出:

exceptions.OptimizationError – if problem is not solvable by cvxpy

add_constraint(new_constraint)

在优化问题中加入一个新的约束条件。这个约束必须满足 DCP 规则，即要么是一个线性平等约束，要么是凸不平等约束。

例如:

ef.add_constraint(lambda x : x[0] == 0.02)
ef.add_constraint(lambda x : x >= 0.01)
ef.add_constraint(lambda x: x <= np.array([0.01, 0.08, ..., 0.5]))

参数:

new_constraint (callable (e.g lambda function)) – the constraint to be added

add_objective(new_objective, **kwargs)

在目标函数中添加一个新项。这个项必须是凸的，并由 cvxpy 原子函数构建。

例如:

def L1_norm(w, k=1):
    return k * cp.norm(w, 1)

ef.add_objective(L1_norm, k=2)

参数:

new_objective (cp.Expression (i.e function of cp.Variable)) – the objective to be added

add_sector_constraints(sector_mapper, sector_lower, sector_upper)

对不同资产组的权重总和添加限制。最常见的是行业限制，例如，投资组合中的科技风险必须低于 x%:

sector_mapper = {
    "GOOG": "tech",
    "FB": "tech",,
    "XOM": "Oil/Gas",
    "RRC": "Oil/Gas",
    "MA": "Financials",
    "JPM": "Financials",
}

sector_lower = {"tech": 0.1}  # at least 10% to tech
sector_upper = {
    "tech": 0.4, # less than 40% tech
    "Oil/Gas": 0.1 # less than 10% oil and gas
}

参数:

• sector_mapper ({str: str} dict) – dict that maps tickers to sectors

• sector_lower ({str: float} dict) – lower bounds for each sector

• sector_upper ({str:float} dict) – upper bounds for each sector

convex_objective(custom_objective, weights_sum_to_one=True, **kwargs)

优化一个自定义的凸型目标函数。应使用 ef.add_constraint() 添加约束条件。优化器的参数必须作为 keyword-args 传递。例如:

# Could define as a lambda function instead
def logarithmic_barrier(w, cov_matrix, k=0.1):
    # 60 Years of Portfolio Optimization, Kolm et al (2014)
    return cp.quad_form(w, cov_matrix) - k * cp.sum(cp.log(w))

w = ef.convex_objective(logarithmic_barrier, cov_matrix=ef.cov_matrix)

参数:

• custom_objective (function with signature (cp.Variable, **kwargs) -> cp.Expression) – an objective function to be MINIMISED. This should be written using cvxpy atoms Should map (w, **kwargs) -> float.

• weights_sum_to_one (bool, optional) – whether to add the default objective, defaults to True

抛出:

OptimizationError – if the objective is nonconvex or constraints nonlinear.

返回:

asset weights for the efficient risk portfolio

返回类型:

OrderedDict

deepcopy()

返回优化器的自定义深度拷贝。这是必要的，因为 cvxpy 表达式不支持深度拷贝，但是为了避免意外的副作用，需要拷贝可变参数。 相反，我们创建一个优化器的浅层副本，然后手动复制可变参数。

nonconvex_objective(custom_objective, objective_args=None, weights_sum_to_one=True, constraints=None, solver='SLSQP', initial_guess=None)

使用 scipy 后端优化一些目标函数。这可以支持非凸目标和非线性约束，但可能会卡在局部最小值。例如:

# Market-neutral efficient risk
constraints = [
    {"type": "eq", "fun": lambda w: np.sum(w)},  # weights sum to zero
    {
        "type": "eq",
        "fun": lambda w: target_risk ** 2 - np.dot(w.T, np.dot(ef.cov_matrix, w)),
    },  # risk = target_risk
]
ef.nonconvex_objective(
    lambda w, mu: -w.T.dot(mu),  # min negative return (i.e maximise return)
    objective_args=(ef.expected_returns,),
    weights_sum_to_one=False,
    constraints=constraints,
)

参数:

• objective_function (function with signature (np.ndarray, args) -> float) – an objective function to be MINIMISED. This function should map (weight, args) -> cost

• objective_args (tuple of np.ndarrays) – arguments for the objective function (excluding weight)

• weights_sum_to_one (bool, optional) – whether to add the default objective, defaults to True

• constraints (dict list) – list of constraints in the scipy format (i.e dicts)

• solver (string) – which SCIPY solver to use, e.g “SLSQP”, “COBYLA”, “BFGS”. User beware: different optimizers require different inputs.

• initial_guess (np.ndarray) – the initial guess for the weights, shape (n,) or (n, 1)

返回:

asset weights that optimize the custom objective

返回类型:

OrderedDict

参考文献

[1]

López de Prado, M. (2016). Building Diversified Portfolios that Outperform Out of Sample. The Journal of Portfolio Management, 42(4), 59–69.

[2]

Bailey and Loópez de Prado (2013). An Open-Source Implementation of the Critical-Line Algorithm for Portfolio Optimization