用户指南

这个操作指南，主要针对那些对优化组合一些资产（很可能是股票）的快速方法感兴趣的用户。 在必要的时候，我也介绍了所需的理论，也指出了可能是更高级优化技术的合适跳板的领域。 有关参数的细节可以在各自的文档页面中找到（请见侧边导航栏）。

在本指南中，我们将专注于均值-方差优化（MVO），这是大多数人听到“投资组合优化”时想到的东西。 MVO 构成了 PyPortfolioOpt 产品的核心，不过需要注意的是，MVO 有很多种类，可能有非常不同的性能特征。 请参考侧边导航栏，了解各种可能性，以及提供的其他优化方法。现在，我们将继续使用标准的有效前沿。

PyPortfolioOpt 的设计考虑到了模块化，下面的流程图总结了 PyPortfolioOpt 目前的功能和整体布局。

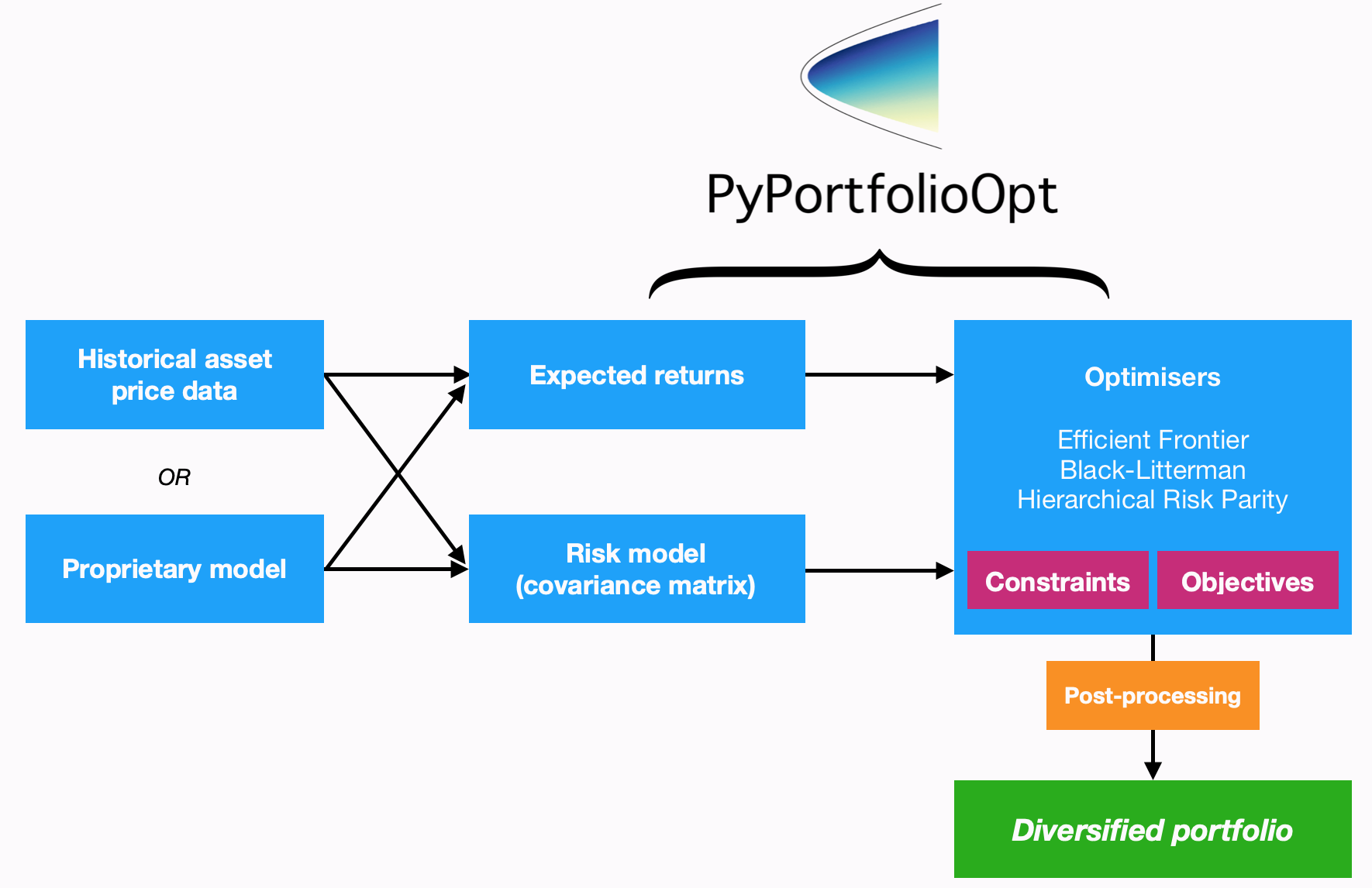
PyPortfolioOpt库的概念流程图

处理历史价格

均值方差优化需要两样原材料：资产的期望收益和协方差矩阵（或者更一般地说，一个风险模型）。 PyPortfolioOpt 提供了估算这两项的方法（位于 expected_returns 和 risk_models 中），同时也支持用户使用自己的模型。

最开始，我认为大多数用户会更喜欢使用内置的模型。 这时，所需要提供的是资产的历史价格数据。数据应该看起来像下面这样:

                XOM        RRC        BBY         MA        PFE        JPM
date
2010-01-04  54.068794  51.300568  32.524055  22.062426  13.940202  35.175220
2010-01-05  54.279907  51.993038  33.349487  21.997149  13.741367  35.856571
2010-01-06  54.749043  51.690697  33.090542  22.081820  13.697187  36.053574
2010-01-07  54.577045  51.593170  33.616547  21.937523  13.645634  36.767757
2010-01-08  54.358093  52.597733  32.297466  21.945297  13.756095  36.677460

索引应该由日期或时间戳组成，每一列应该代表一种资产的价格的时间序列。在 GitHub repo 的 测试文件夹 中已经包含了一个真实的股票价格数据集。

备注

价格数据不一定是日频的，但应该保证所有资产的频率应该是一样的（存在变通办法，但不优雅）。

在将历史价格读入 pandas dataframe 变量 df 后，下一步需要选择估计期望收益和协方差矩阵的函数。默认方法是 expected_returns.mean_historical_return() 和 risk_models.CovarianceShrinkage 中的 Ledoit Wolf 收缩协方差矩阵估计。将这两个函数应用到历史数据上:

from pypfopt.expected_returns import mean_historical_return
from pypfopt.risk_models import CovarianceShrinkage

mu = mean_historical_return(df)
S = CovarianceShrinkage(df).ledoit_wolf()

mu 是每个资产的估计期望收益（pandas series），S 是估计的协方差矩阵（部分内容如下所示）:

        GOOG      AAPL        FB      BABA      AMZN        GE       AMD  \
GOOG  0.045529  0.022143  0.006389  0.003720  0.026085  0.015815  0.021761
AAPL  0.022143  0.207037  0.004334  0.002954  0.058200  0.038102  0.084053
FB    0.006389  0.004334  0.029233  0.003770  0.007619  0.003008  0.005804
BABA  0.003720  0.002954  0.003770  0.013438  0.004176  0.002011  0.006332
AMZN  0.026085  0.058200  0.007619  0.004176  0.276365  0.038169  0.075657
GE    0.015815  0.038102  0.003008  0.002011  0.038169  0.083405  0.048580
AMD   0.021761  0.084053  0.005804  0.006332  0.075657  0.048580  0.388916

现在我们有了期望收益和风险模型，我们准备进入实际的投资组合优化。

均值-方差优化

均值-方差优化是基于哈里-马科维茨1952年的经典论文 [1] ，它将投资组合管理从一门艺术转变为一门科学。 其关键的理论是，将具有不同期望收益和波动率的资产结合起来，人们可以计算出一个数学上的最佳配置。

如果 \(w\) 是具有期望收益 \(\mu\) 的股票的权重向量，则投资组合的收益率等于每只股票的权重乘以其收益率，即 \(w^T \mu\) 。 以协方差矩阵 \(\Sigma\) 表示的投资组合风险为 \(w^T \Sigma w\) 。 投资组合优化可以被视为一个凸优化问题，可以使用二次规划找到解。 如果我们把目标收益率表示为 \(\mu^*\) ，则长期投资组合优化问题的表述如下：

\[\begin{split}\begin{equation*} \begin{aligned} & \underset{w}{\text{minimise}} & & w^T \Sigma w \\ & \text{subject to} & & w^T\mu \geq \mu^*\\ &&& w^T\mathbf{1} = 1 \\ &&& w_i \geq 0 \\ \end{aligned} \end{equation*}\end{split}\]

如果我们改变目标收益，我们将得到一组不同的权重（即不同的投资组合），所有这些最佳投资组合的集合被称为有效前沿。

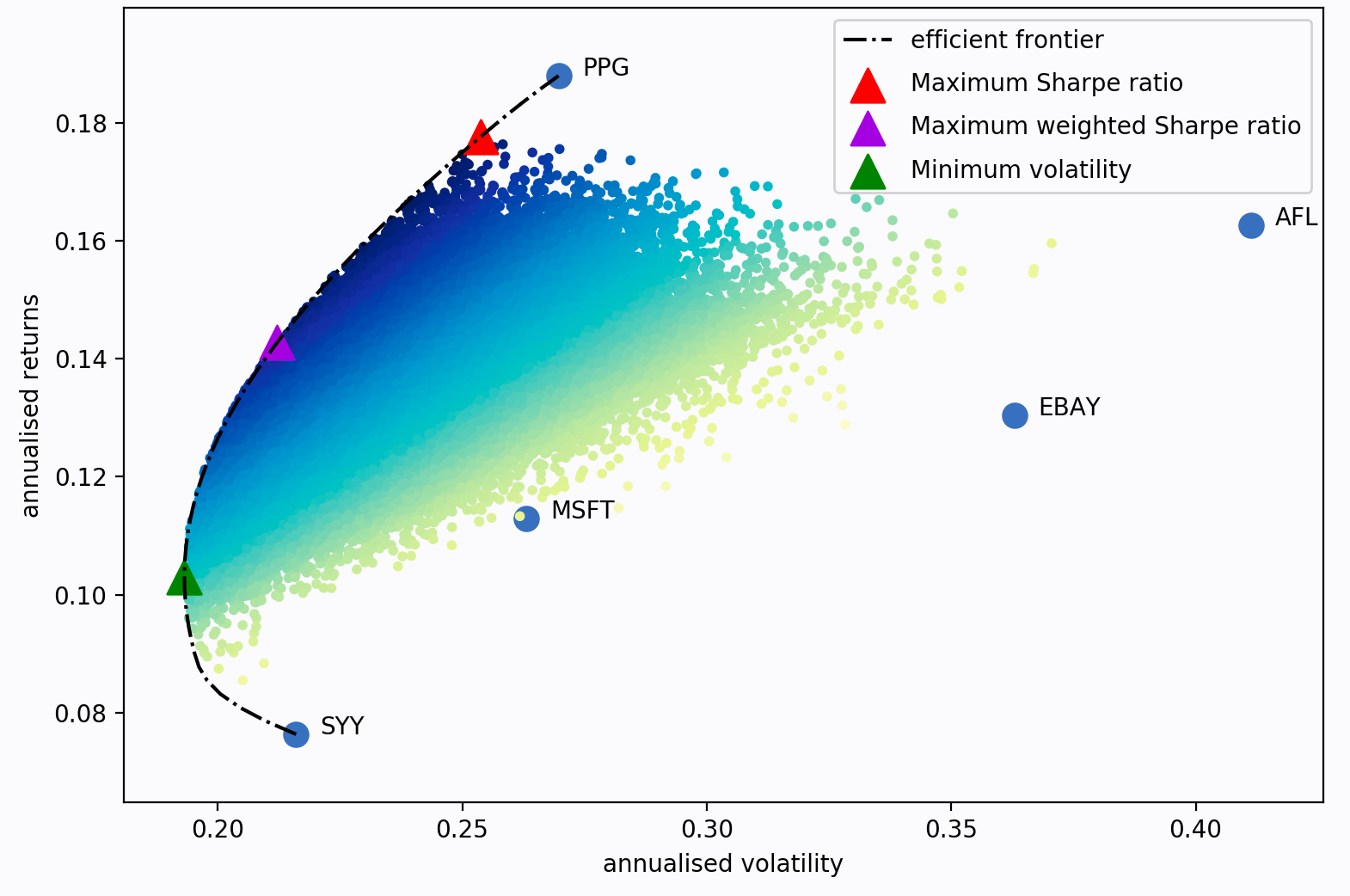
risk-return characteristics of possible portfolios

这张图上的每个点代表可能的投资组合，深蓝色代表“更好”的组合（以夏普比率评估）。 黑色虚线是有效前沿本身。三角形标记代表不同优化目标的最佳投资组合。

夏普比率指在承担了每单位风险（波动率）下超过无风险利率的收益。

\[SR = \frac{R_P - R_f}{\sigma}\]

它的形式很重要，它衡量了是投资组合的收益，并对风险进行调整。 在实践中，与其在给定的目标收益率下试图最小化波动率（按照 Markowitz 1952 的说法），不如直接找到最大夏普比率，那更有意义。 这在 EfficientFrontier 类中通过 max_sharpe() 方法实现。使用之前的系列 mu 和数据框架 S:

from pypfopt.efficient_frontier import EfficientFrontier

ef = EfficientFrontier(mu, S)
weights = ef.max_sharpe()

如果 print 这些权重，会得到一个浮点数很长的的结果，它们是优化器的原始输出。 建议使用 clean_weights() 方法，该方法将微小的权重截断为零，并对其余部分进行舍入:

cleaned_weights = ef.clean_weights()
ef.save_weights_to_file("weights.txt")  # saves to file
print(cleaned_weights)

将输出:

{'GOOG': 0.01269,
'AAPL': 0.09202,
'FB': 0.19856,
'BABA': 0.09642,
'AMZN': 0.07158,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.06129,
'MA': 0.24562,
'PFE': 0.18413,
'JPM': 0.0,
'SBUX': 0.03769}

如果我们想知道具有最佳权重 w 的投资组合的绩效表现，可以调用 portfolio_performance() 方法:

ef.portfolio_performance(verbose=True)

Expected annual return: 33.0%
Annual volatility: 21.7%
Sharpe Ratio: 1.43

关于优化参数的详细讨论在 通用有效前沿 中也说明。 还有有两个需要注意的地方，将在下面说明。

空头仓位

为了允许做空，只需用允许负权重的边界来初始化 EfficientFrontier 对象，比如:

ef = EfficientFrontier(mu, S, weight_bounds=(-1,1))

这可以用来生成市场中性投资组合（权重之和为零），但由于数学计算原因，这些投资组合只适用于 efficient_risk() 和 efficient_return() 优化方法。 如果想要一个市场中性的投资组合，请传递 market_neutral=True，如下图所示:

ef.efficient_return(target_return=0.2, market_neutral=True)

处理零权重

根据经验，我发现均值-方差优化经常将许多资产权重设置为零。 无论是出于多样化的目的还是其他原因，如果需要在投资组合中拥有一定数量的头寸，这可能不理想。

为了解决这个问题，我引入了一个目标函数，它借用了机器学习中的正则化思想。 从本质上讲，通过给目标添加一个额外的成本函数，可以“鼓励”优化器选择不同的权重（数学细节在更多关于 更多关于 L2 正则化的内容 部分提供）。 要使用这个功能，请改变 gamma 参数:

from pypfopt import objective_functions

ef = EfficientFrontier(mu, S)
ef.add_objective(objective_functions.L2_reg, gamma=0.1)
w = ef.max_sharpe()
print(ef.clean_weights())

结果是，零权重比以前少得多:

{'GOOG': 0.06366,
'AAPL': 0.09947,
'FB': 0.15742,
'BABA': 0.08701,
'AMZN': 0.09454,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.01766,
'BAC': 0.0,
'GM': 0.0,
'T': 0.00398,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.03072,
'RRC': 0.00737,
'BBY': 0.07572,
'MA': 0.1769,
'PFE': 0.12346,
'JPM': 0.0,
'SBUX': 0.06209}

后期处理

在实践中，我们需要将这些权重转换为实际下单数量，告诉你每种资产该购买多少。 将在 后期处理 中进一步讨论，这里提供一个简单的例子:

from pypfopt.discrete_allocation import DiscreteAllocation, get_latest_prices

latest_prices = get_latest_prices(df)
da = DiscreteAllocation(w, latest_prices, total_portfolio_value=20000)
allocation, leftover = da.lp_portfolio()
print(allocation)

这是建立 $20,000 投资组合应该购买的股票数量:

{'AAPL': 2.0,
'FB': 12.0,
'BABA': 14.0,
'GE': 18.0,
'WMT': 40.0,
'GM': 58.0,
'T': 97.0,
'SHLD': 1.0,
'XOM': 47.0,
'RRC': 3.0,
'BBY': 1.0,
'PFE': 47.0,
'SBUX': 5.0}

提高表现

假设已经进行了回测，但结果并不理想，应该尝试做些什么？

  • 可以试试层次风险平价模型（见 其他优化 ），它的表现似乎在样本外稳定地超过了的均值-方差优化。

  • 使用 Black-Litterman 模型来构建一个更稳定的期望收益模型。或者，干脆完全放弃期望收益率。有大量研究表明，最小方差组合（ef.min_volatility()）在样本外始终优于最大夏普比率组合（即使以夏普比率衡量），因为预测期望收益有难度。

  • 尝试不同的风险模型：众所周知，与样本协方差矩阵相比，收缩模型具有更好的数值特性。

  • 添加一些新的目标项或约束条件。调整 L2 正则化参数，看看多样化对绩效的影响。

至此，指南结束。请前往侧边导航栏的相应部分，了解更多 PyPortfolioOpt 提供的不同模型的参数和理论细节。 如果有任何问题，请在 GitHub 上提出问题，我将尽力回复。

如果想了解更多的例子，请查看 cookbook 。

参考文献