绘图
EfficientFrontier 中的所有优化函数都会产生一个单一的最优组合。
你可能想要绘制整个有效前沿,这个有效前沿有几种被理解的方式:
一系列目标风险的所有
efficient_risk()投资组合的集合。一系列目标收益的所有
efficient_return()投资组合的集合。一系列风险厌恶者的所有
max_quadratic_utility()投资组合的集合。
plotting 模块为这三种方法提供了支持。
为了绘制有效前沿,应该实例化 EfficientFrontier 对象,并像通常那样添加约束条件,不同的是在调用优化函数(如
ef.max_sharpe())之前,应该将这个实例化的对象传递给 plot.plot_efficient_frontier():
ef = EfficientFrontier(mu, S, weight_bounds=(None, None))
ef.add_constraint(lambda w: w[0] >= 0.2)
ef.add_constraint(lambda w: w[2] == 0.15)
ef.add_constraint(lambda w: w[3] + w[4] <= 0.10)
fig, ax = plt.subplots()
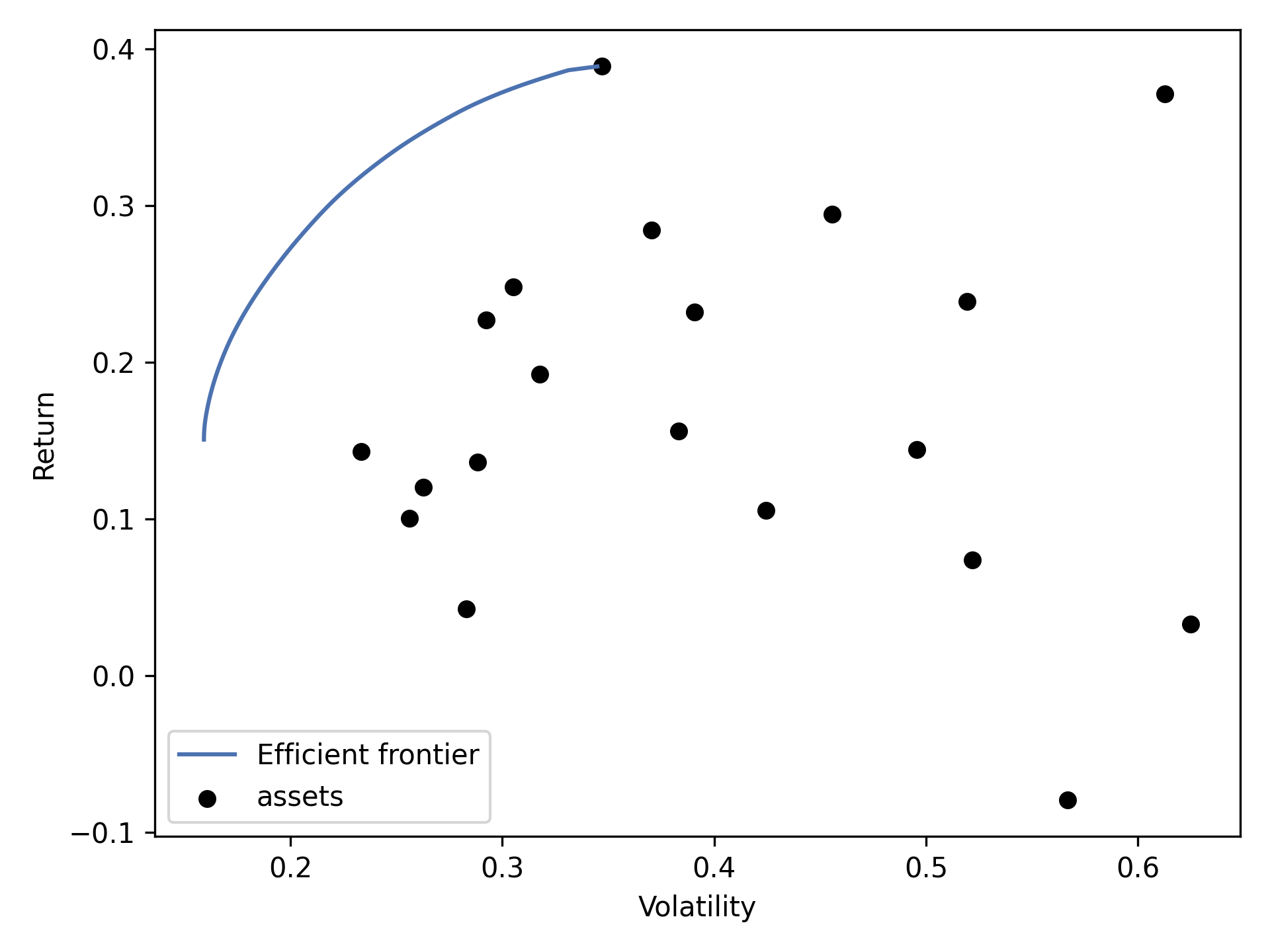
plotting.plot_efficient_frontier(ef, ax=ax, show_assets=True)
plt.show()
将产生以下图片:
可以明确地传递一个参数范围(风险、效用或收益)来生成一个前沿:
# 100 portfolios with risks between 0.10 and 0.30
risk_range = np.linspace(0.10, 0.40, 100)
plotting.plot_efficient_frontier(ef, ef_param="risk", ef_param_range=risk_range,
show_assets=True, showfig=True)
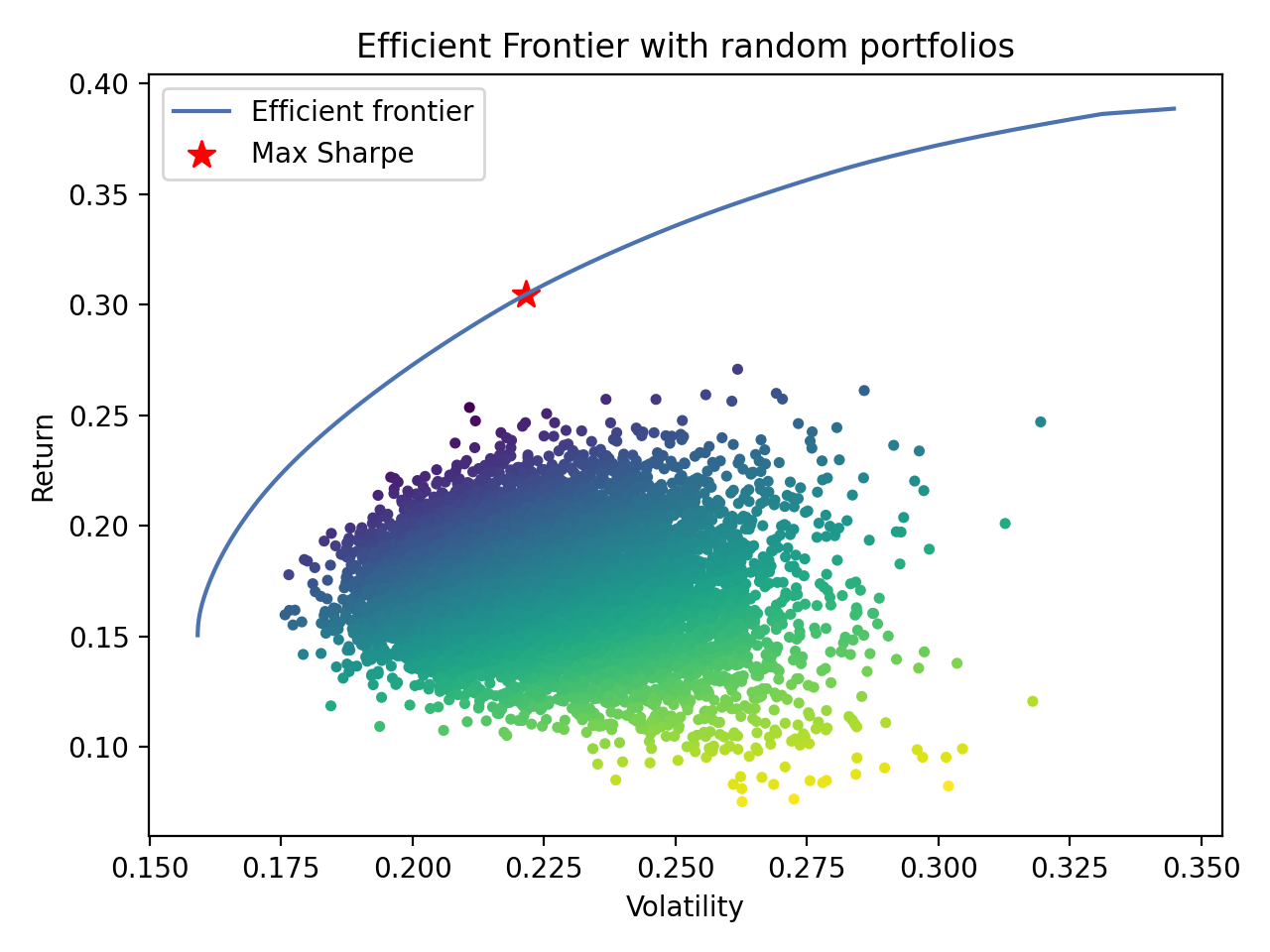
我们也可以很容易地生成更复杂的图。下面的脚本绘制了有效前沿和随机生成的(次优)投资组合,夏普比率根据值不同而颜色不同:
fig, ax = plt.subplots()
ef_max_sharpe = ef.deepcopy()
plotting.plot_efficient_frontier(ef, ax=ax, show_assets=False)
# Find the tangency portfolio
ef_max_sharpe.max_sharpe()
ret_tangent, std_tangent, _ = ef_max_sharpe.portfolio_performance()
ax.scatter(std_tangent, ret_tangent, marker="*", s=100, c="r", label="Max Sharpe")
# Generate random portfolios
n_samples = 10000
w = np.random.dirichlet(np.ones(ef.n_assets), n_samples)
rets = w.dot(ef.expected_returns)
stds = np.sqrt(np.diag(w @ ef.cov_matrix @ w.T))
sharpes = rets / stds
ax.scatter(stds, rets, marker=".", c=sharpes, cmap="viridis_r")
# Output
ax.set_title("Efficient Frontier with random portfolios")
ax.legend()
plt.tight_layout()
plt.savefig("ef_scatter.png", dpi=200)
plt.show()
将输出: