风险模型

除了期望收益外，均值-方差优化还需要一个风险模型，即量化资产风险的某种方式。 最常用的风险模型是协方差矩阵，它描述了资产的波动性和它们的一致性。 这一点很重要，因为分散投资的原则之一是，通过做许多不相关的赌注可以减少风险（相关系数只是归一化的协方差）。

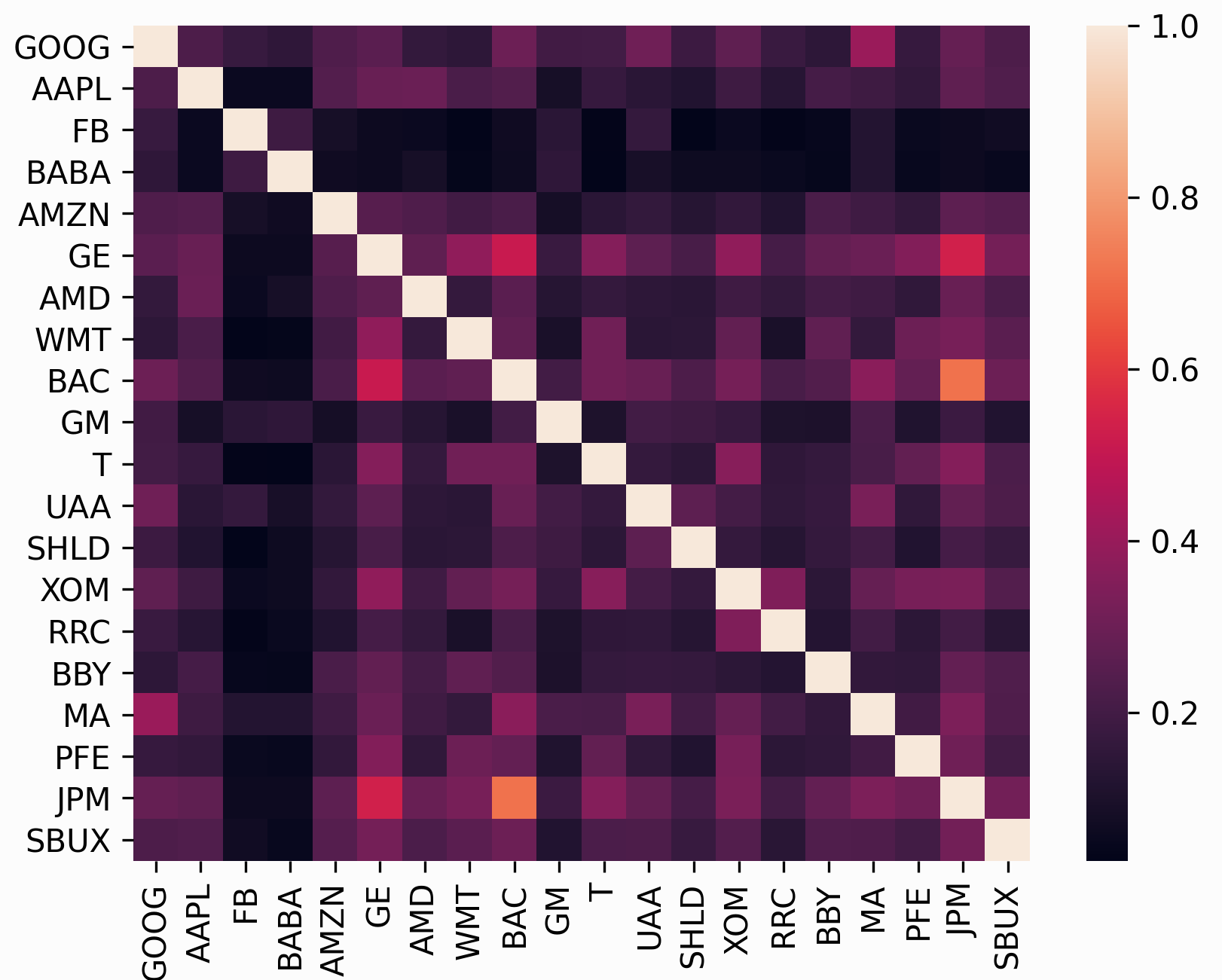
在许多方面，风险模型的主题比期望收益的主题重要得多，因为历史方差通常是一个比历史平均收益更持久的统计数据。 事实上，Kritzman 等人（2010） [1] 的研究 表明，通过优化而不提供期望收益形成的最小方差组合，在样本外的表现实际上要好得多。

但问题是，在实践中我们无法获得协方差矩阵（就像我们无法获得期望收益一样），我们唯一能做的就是根据过去的数据进行估计。 最直接的方法是根据历史收益率计算样本协方差矩阵，最近（2000年后）的研究表明，协方差矩阵有更稳健的统计估计。 除了为 sklearn 中的估计器提供包装外，PyPortfolioOpt 还提供了一些实验性的替代方法，如半方差和指数加权协方差。

注意

协方差矩阵的估计是一个非常深入和活跃研究的课题，涉及统计学、计量经济学和数值计算方法。 PyPortfolioOpt 实现了几个选项，但还有很大的空间来实现更多的复杂性。

risk_models 模块提供了在给定历史收益率的情况下估计协方差矩阵的函数。

数据输入的格式与 期望收益率 中的相同。

目前已经实现：

• 固定非半正定矩阵

• 一般风险矩阵函数，允许调用一个函数来运行风险模型。

• 样本协方差

• 半方差

• 指数加权协方差

• 最小协方差决定数

• 缩减协方差矩阵：

  • 手动收缩

  • Ledoit Wolf 收缩

  • Oracle 近似收缩

• 协方差到相关矩阵

备注

对于这些方法，如果你希望传入收益率（默认是价格），请设置布尔参数 returns_data=True 。

pypfopt.risk_models.risk_matrix(prices, method='sample_cov', **kwargs)

计算协方差矩阵，风险模型以 method 参数指定。

参数:

• prices (pd.DataFrame) – 调整后的资产收盘价，每一行是一个日期，每一列是一个股票/ID。

• returns_data (bool, 默认为 False.) – 如果是 true, 第一个参数是收益率而不是价格

• method (str, optional) –

  要使用的风险模型。应该是其中一个:

  • sample_cov

  • semicovariance

  • exp_cov

  • ledoit_wolf

  • ledoit_wolf_constant_variance

  • ledoit_wolf_single_factor

  • ledoit_wolf_constant_correlation

  • oracle_approximating

抛出:

NotImplementedError – 如果 method 错误

返回:

年化样本协方差矩阵

返回类型:

pd.DataFrame

pypfopt.risk_models.fix_nonpositive_semidefinite(matrix, fix_method='spectral')

检查协方差矩阵是否为半正定矩阵，如果不是，就用所选的方法修正它。 spectral 将负的特征值设置为零，然后重建矩阵，而 diag 法在对角线上增加一个小的正值。

参数:

• matrix (pd.DataFrame) – 原始协方差矩阵（不是 PSD）

• fix_method (str, optional) – {“spectral”, “diag”}, 默认为 “spectral”

抛出:

NotImplementedError – 如果 method 方法未实现

返回:

半正定协方差矩阵

返回类型:

pd.DataFrame

并非所有计算出来的协方差矩阵都是半正定矩阵（PSD）。这个方法检查一个矩阵是否是 PSD，如果不是，则对其进行修复。

pypfopt.risk_models.sample_cov(prices, returns_data=False, frequency=252, log_returns=False, **kwargs)

计算（日频）资产收益的年化样本协方差矩阵。

参数:

• prices (pd.DataFrame) – 调整后的资产收盘价，每一行是一个日期，每一列是一个股票/ID。

• returns_data (bool, 默认为 False.) – 如果是 true, 第一个参数是收益率而不是价格

• frequency (int, optional) – 一年中的时间数，默认为252（一年中的交易日数）。

• log_returns (bool, 默认为 False) – 是否使用对数收益进行计算

返回:

年化样本协方差矩阵

返回类型:

pd.DataFrame

这是课本上的默认方法，样本协方差矩阵（我们表示为 S）中的条目是第 i 项和第 j 项资产之间的样本协方差（对角线由方差组成）。 尽管样本协方差矩阵是协方差矩阵的无偏估计，即 \(E(S) = \Sigma\)。 但在实践中，它存在着错误的 misspecification error 和缺乏稳健性。 这在均值-方差优化中特别有问题，因为优化器可能会对错误的值给予额外的权重。

备注

这不应该是默认选择! 请使用收缩估计来代替。

pypfopt.risk_models.semicovariance(prices, returns_data=False, benchmark=7.9e-05, frequency=252, log_returns=False, **kwargs)

估算半方差矩阵，即收益率低于基准的协方差。

参数:

• prices (pd.DataFrame) – 调整后的资产收盘价，每一行是一个日期，每一列是一个股票/ID。

• returns_data (bool, defaults to False.) – 如果是 true, 第一个参数是收益率而不是价格

• benchmark (float) – 基准收益，默认为每日无风险利率，即 \(1.02^{(1/252)} -1\) 。

• frequency (int, optional) – 一年中的时间数，默认为252（一年中的交易日数）。确保你使用适当的基准，例如，如果 frequency=12 ，使用月度无风险利率。

• log_returns (bool, 默认为 False) – 是否使用对数收益进行计算

返回:

半方差矩阵

返回类型:

pd.DataFrame

半方差是指所有低于某个基准 B（通常是无风险利率）的收益的方差，它是衡量下行风险的一个常用指标。 半方差矩阵有多种定义方式，主要的区别在于 pairwise 的性质，即我们应该对 \(\min(r_i,B)\min(r_j,B)\) 还是 \(\min(r_ir_j, B)\) 求和。在实现中，我们遵循 Estrada（2007） [2] 的建议，倾向于：

\[\frac{1}{n}\sum_{i = 1}^n {\sum_{j = 1}^n {\min \left( {{r_i},B} \right)} } \min \left( {{r_j},B} \right)\]

pypfopt.risk_models.exp_cov(prices, returns_data=False, span=180, frequency=252, log_returns=False, **kwargs)

估算指数加权的协方差矩阵，该矩阵对最近的数据给予更大的权重。

参数:

• prices (pd.DataFrame) – 调整后的资产收盘价，每一行是一个日期，每一列是一个股票/ID。

• returns_data – 如果是 true，则第一个参数是收益率，而不是价格

• span (int, optional) – 指数加权函数的跨度，默认为 180

• frequency (int, optional) – 一年中的时间数，默认为252（一年中的交易日数）。

• log_returns (bool, 默认为 False) – 是否使用对数收益率进行计算

返回:

指数协方差矩阵的年化估计值

返回类型:

pd.DataFrame

指数协方差矩阵是一种新颖的方式，在计算协方差时给予最近的数据更多的权重，就像指数移动平均和比简单平均相比一样。 关于这个估计器的完整解释，请参考我学术网站上的 文章 。

pypfopt.risk_models.cov_to_corr(cov_matrix)

将一个协方差矩阵转换为一个相关矩阵。

参数:

cov_matrix (pd.DataFrame) – 协方差矩阵

返回:

相关矩阵

返回类型:

pd.DataFrame

pypfopt.risk_models.corr_to_cov(corr_matrix, stdevs)

将相关矩阵转换为协方差矩阵

参数:

• corr_matrix (pd.DataFrame) – 相关矩阵

• stdevs (array-like) – 标准差的向量

返回:

协方差矩阵

返回类型:

pd.DataFrame

收缩估计

对于那些有兴趣了解收缩估计器的人来说，一个很好的入门阅读是 Ledoit 和 Wolf 的 Honey, I Shrunk the Sample Covariance Matrix [3] ，它很好地讲述了背后的原理，我们将采用其中使用的概念。 我写了一篇这篇文章的摘要，可以在 我的网站 上找到。 在 Ledoit and Wolf (2001) [4] 中可以找到更严肃的参考。

其基本思想是，无偏但往往估计不足的样本协方差可以与结构化估计器 \(F\) 相结合，使用下面的公式（其中 \(\delta\) 是收缩常数）：

\[\hat{\Sigma} = \delta F + (1-\delta) S\]

它之所以被称为收缩，是因为它可以被认为是将样本的协方差矩阵“收缩”到另一个估计值，因此被称为收缩目标。 收缩目标可能有大偏差小误差。该目标有许多可能的选项，每一个选项都会导致不同的最佳收缩常数 \(delta\) 。 PyPortfolioOpt 提供以下收缩方法：

• Ledoit-Wolf 收缩：

  • constant_variance 收缩，即目标是对角矩阵，对角线上是资产方差的平均值，其他地方为零。这是 sklearn.LedoitWolf 提供的收缩。

  • single_factor 收缩，基于夏普的单指数模型，该模型有效地使用股票对市场的 β 值作为风险模型。参见 Ledoit and Wolf 2001 [4] 。

  • constant_correlation 收缩，其中所有成对的相关性被设置为平均相关性（样本方差不变）。参见 Ledoit and Wolf 2003 [3] 。

• Oracle 近似收缩（OAS），由 Chen 等人（2010） [5] 提出，当样本是高斯或接近高斯时，它的均方误差比 Ledoit-Wolf 收缩低。

小技巧

对于大多数情况，我只用 Ledoit Wolf 收缩，正如 Quantopian 在他们的量化金融系列讲座中所推荐的。

本开源库的实现，是在 xtuanta 的帮助下， 从 Michael Wolf’s webpage 的 Matlab 代码翻译过来的。

class pypfopt.risk_models.CovarianceShrinkage(prices, returns_data=False, frequency=252, log_returns=False)

提供计算协方差矩阵的收缩估计的方法，使用样本协方差矩阵，并选择结构化估计器为单位矩阵乘以平均样本方差。 收缩常数可以手动输入，也存在估计最优值的方法（推荐 Ledoit Wolf）。

Instance variables:

• X - pd.DataFrame (收益率)

• S - np.ndarray (样本协方差矩阵)

• delta - float (收缩常数)

• frequency - int

__init__(prices, returns_data=False, frequency=252, log_returns=False)

参数:

• prices (pd.DataFrame) – 调整后的资产收盘价，每一行是一个日期，每一列是一个股票/ID。

• returns_data (bool, 默认为 False.) – 如果是 true, 则第一个参数是收益率而不是价格

• frequency (int, optional) – 一年中的时间段数，默认为252（一年中的交易日数）

• log_returns (bool, 默认为 False) – 是否使用对数收益进行计算

ledoit_wolf(shrinkage_target='constant_variance')

计算特定收缩目标的 Ledoit-Wolf 收缩估计值。

参数:

shrinkage_target (str, optional) – 收缩目标选项, constant_variance、 single_factor 或 constant_correlation. 默认为 constant_variance.

抛出:

NotImplementedError – 如果 shrinkage_target 错误

返回:

收缩样本协方差矩阵

返回类型:

np.ndarray

oracle_approximating()

计算 Oracle 近似收缩的估算值

返回:

收缩样本协方差矩阵

返回类型:

np.ndarray

shrunk_covariance(delta=0.2)

将一个样本协方差矩阵缩减为单位矩阵（按平均样本方差缩放）。 这种方法并不估计最佳收缩参数，它需要手动输入。

参数:

delta (float, optional) – 收缩参数, 默认为 0.2.

返回:

收缩样本的协方差矩阵

返回类型:

np.ndarray

参考文献

[1]

Kritzman, Page & Turkington (2010) In defense of optimization: The fallacy of 1/N. Financial Analysts Journal, 66(2), 31-39.

[2]

Estrada (2006), Mean-Semivariance Optimization: A Heuristic Approach

[3] (1,2)

Ledoit, O., & Wolf, M. (2003). Honey, I Shrunk the Sample Covariance Matrix The Journal of Portfolio Management, 30(4), 110–119. https://doi.org/10.3905/jpm.2004.110

[4] (1,2)

Ledoit, O., & Wolf, M. (2001). Improved estimation of the covariance matrix of stock returns with an application to portfolio selection, 10, 603–621.

[5]

Chen et al. (2010), Shrinkage Algorithms for MMSE Covariance Estimation, IEEE Transactions on Signals Processing, 58(10), 5016-5029.