绘图函数

该模块的功能允许我们创建图表，以帮助我们快速分析最佳投资组合的属性。 帮助我们快速分析我们的最优投资组合的属性。

下面的例子构建了投资组合和有效边界，并将使用本模块的函数来绘制。 将使用本模块的函数来绘制。

例子

import numpy as np
import pandas as pd
import yfinance as yf
import riskfolio as rp

# Date range
start = '2016-01-01'
end = '2019-12-30'

# Tickers of assets
tickers = ['JCI', 'TGT', 'CMCSA', 'CPB', 'MO', 'APA', 'MMC', 'JPM',
           'ZION', 'PSA', 'BAX', 'BMY', 'LUV', 'PCAR', 'TXT', 'TMO',
           'DE', 'MSFT', 'HPQ', 'SEE', 'VZ', 'CNP', 'NI', 'T', 'BA']
tickers.sort()

# Downloading the data
data = yf.download(tickers, start = start, end = end)
data = data.loc[:,('Adj Close', slice(None))]
data.columns = tickers
assets = data.pct_change().dropna()

Y = assets

# Creating the Portfolio Object
port = rp.Portfolio(returns=Y)

# To display dataframes values in percentage format
pd.options.display.float_format = '{:.4%}'.format

# Choose the risk measure
rm = 'MSV'  # Semi Standard Deviation

# Estimate inputs of the model (historical estimates)
method_mu='hist' # Method to estimate expected returns based on historical data.
method_cov='hist' # Method to estimate covariance matrix based on historical data.

port.assets_stats(method_mu=method_mu, method_cov=method_cov, d=0.94)

# Estimate the portfolio that maximizes the risk adjusted return ratio
w1 = port.optimization(model='Classic', rm=rm, obj='Sharpe', rf=0.0, l=0, hist=True)

# Estimate points in the efficient frontier mean - semi standard deviation
ws = port.efficient_frontier(model='Classic', rm=rm, points=20, rf=0, hist=True)

# Estimate the risk parity portfolio for semi standard deviation
w2 = port.rp_optimization(model='Classic', rm=rm, rf=0, b=None, hist=True)

模块函数

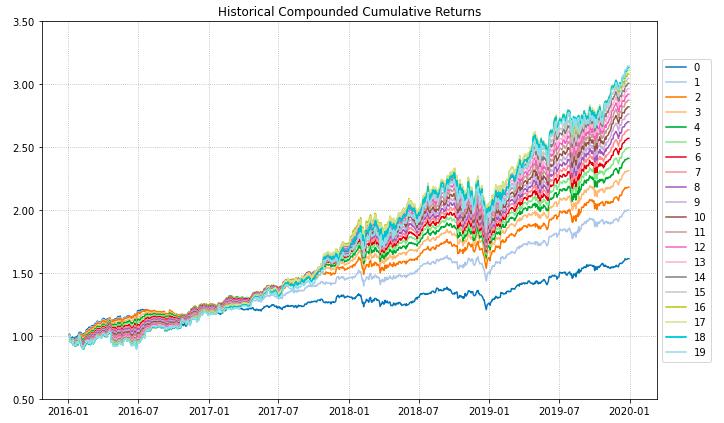
PlotFunctions.plot_series(returns, w, cmap='tab20', n_colors=20, height=6, width=10, ax=None)

Create a chart with the compounded cumulative of the portfolios.

参数:

• returns (DataFrame) – Assets returns.

• w (DataFrame of shape (n_assets, n_portfolios)) – Portfolio weights.

• cmap (cmap, optional) – Colorscale used to plot each portfolio compounded cumulative return. The default is ‘tab20’.

• n_colors (int, optional) – Number of distinct colors per color cycle. If there are more assets than n_colors, the chart is going to start to repeat the color cycle. The default is 20.

• height (float, optional) – Height of the image in inches. The default is 6.

• width (float, optional) – Width of the image in inches. The default is 10.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis

示例

ax = rp.plot_series(returns=Y,
                    w=ws,
                    cmap='tab20',
                    height=6,
                    width=10,
                    ax=None)

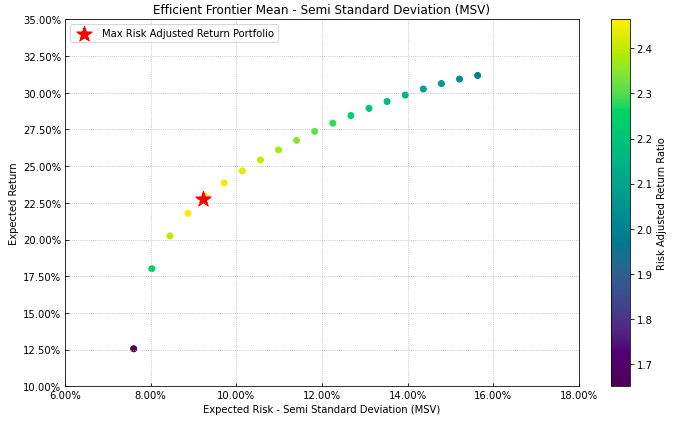
PlotFunctions.plot_frontier(w_frontier, mu, cov=None, returns=None, rm='MV', kelly=False, rf=0, alpha=0.05, a_sim=100, beta=None, b_sim=None, kappa=0.3, solver=None, cmap='viridis', w=None, label='Portfolio', marker='*', s=16, c='r', height=6, width=10, t_factor=252, ax=None)

Creates a plot of the efficient frontier for a risk measure specified by the user.

参数:

• w_frontier (DataFrame) – Portfolio weights of some points in the efficient frontier.

• mu (DataFrame of shape (1, n_assets)) – Vector of expected returns, where n_assets is the number of assets.

• cov (DataFrame of shape (n_features, n_features)) – Covariance matrix, where n_features is the number of features.

• returns (DataFrame of shape (n_samples, n_features)) – Features matrix, where n_samples is the number of samples and n_features is the number of features.

• rm (str, optional) –

  The risk measure used to estimate the frontier. The default is ‘MV’. Possible values are:

  • ’MV’: Standard Deviation.

  • ’KT’: Square Root Kurtosis.

  • ’MAD’: Mean Absolute Deviation.

  • ’MSV’: Semi Standard Deviation.

  • ’SKT’: Square Root Semi Kurtosis.

  • ’FLPM’: First Lower Partial Moment (Omega Ratio).

  • ’SLPM’: Second Lower Partial Moment (Sortino Ratio).

  • ’CVaR’: Conditional Value at Risk.

  • ’TG’: Tail Gini.

  • ’EVaR’: Entropic Value at Risk.

  • ’RLVaR’: Relativistic Value at Risk.

  • ’WR’: Worst Realization (Minimax).

  • ’CVRG’: CVaR range of returns.

  • ’TGRG’: Tail Gini range of returns.

  • ’RG’: Range of returns.

  • ’MDD’: Maximum Drawdown of uncompounded returns (Calmar Ratio).

  • ’ADD’: Average Drawdown of uncompounded cumulative returns.

  • ’DaR’: Drawdown at Risk of uncompounded cumulative returns.

  • ’CDaR’: Conditional Drawdown at Risk of uncompounded cumulative returns.

  • ’EDaR’: Entropic Drawdown at Risk of uncompounded cumulative returns.

  • ’RLDaR’: Relativistic Drawdown at Risk of uncompounded cumulative returns.

  • ’UCI’: Ulcer Index of uncompounded cumulative returns.

• kelly (bool, optional) – Method used to calculate mean return. Possible values are False for arithmetic mean return and True for mean logarithmic return. The default is False.

• rf (float, optional) – Risk free rate or minimum acceptable return. The default is 0.

• alpha (float, optional) – Significance level of VaR, CVaR, EVaR, RLVaR, DaR, CDaR, EDaR, RLDaR and Tail Gini of losses. The default is 0.05.

• a_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of losses. The default is 100.

• beta (float, optional) – Significance level of CVaR and Tail Gini of gains. If None it duplicates alpha value. The default is None.

• b_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of gains. If None it duplicates a_sim value. The default is None.

• kappa (float, optional) – Deformation parameter of RLVaR and RLDaR, must be between 0 and 1. The default is 0.30.

• solver (str, optional) – Solver available for CVXPY that supports power cone programming. Used to calculate RLVaR and RLDaR. The default value is None.

• cmap (cmap, optional) – Colorscale that represents the risk adjusted return ratio. The default is ‘viridis’.

• w (DataFrame of shape (n_assets, 1), optional) – A portfolio specified by the user. The default is None.

• label (str or list, optional) – Name or list of names of portfolios that appear on plot legend. The default is ‘Portfolio’.

• marker (str, optional) – Marker of w. The default is “*”.

• s (float, optional) – Size of marker. The default is 16.

• c (str, optional) – Color of marker. The default is ‘r’.

• height (float, optional) – Height of the image in inches. The default is 6.

• width (float, optional) – Width of the image in inches. The default is 10.

• t_factor (float, optional) –

  Factor used to annualize expected return and expected risks for risk measures based on returns (not drawdowns). The default is 252.

  \[\begin{split}\begin{align} \text{Annualized Return} & = \text{Return} \, \times \, \text{t_factor} \\ \text{Annualized Risk} & = \text{Risk} \, \times \, \sqrt{\text{t_factor}} \end{align}\end{split}\]

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib Axes

示例

label = 'Max Risk Adjusted Return Portfolio'
mu = port.mu
cov = port.cov
returns = port.returns

ax = rp.plot_frontier(w_frontier=ws,
                      mu=mu,
                      cov=cov,
                      returns=returns,
                      rm=rm,
                      rf=0,
                      alpha=0.05,
                      cmap='viridis',
                      w=w1,
                      label=label,
                      marker='*',
                      s=16,
                      c='r',
                      height=6,
                      width=10,
                      t_factor=252,
                      ax=None)

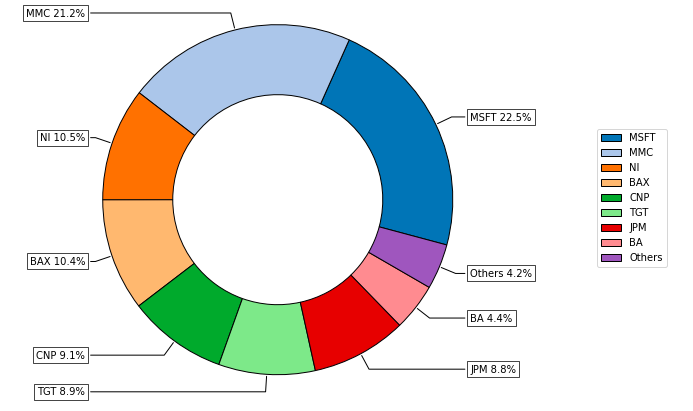
PlotFunctions.plot_pie(w, title='', others=0.05, nrow=25, cmap='tab20', n_colors=20, height=6, width=8, ax=None)

Create a pie chart with portfolio weights.

参数:

• w (DataFrame of shape (n_assets, 1)) – Portfolio weights.

• title (str, optional) – Title of the chart. The default is “”.

• others (float, optional) – Percentage of others section. The default is 0.05.

• nrow (int, optional) – Number of rows of the legend. The default is 25.

• cmap (cmap, optional) – Color scale used to plot each asset weight. The default is ‘tab20’.

• n_colors (int, optional) – Number of distinct colors per color cycle. If there are more assets than n_colors, the chart is going to start to repeat the color cycle. The default is 20.

• height (float, optional) – Height of the image in inches. The default is 10.

• width (float, optional) – Width of the image in inches. The default is 10.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis.

示例

ax = rp.plot_pie(w=w1,
                 title='Portfolio',
                 height=6,
                 width=10,
                 cmap="tab20",
                 ax=None)

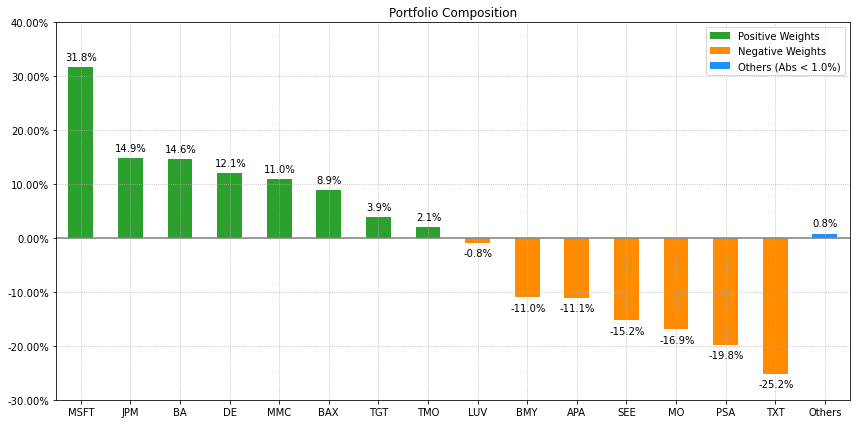
PlotFunctions.plot_bar(w, title='', kind='v', others=0.05, nrow=25, cpos='tab:green', cneg='darkorange', cothers='dodgerblue', height=6, width=10, ax=None)

Create a bar chart with portfolio weights.

参数:

• w (DataFrame of shape (n_assets, 1)) – Portfolio weights.

• title (str, optional) – Title of the chart. The default is “”.

• kind (str, optional) – Kind of bar plot, “v” for vertical bars and “h” for horizontal bars. The default is “v”.

• others (float, optional) – Percentage of others section. The default is 0.05.

• nrow (int, optional) – Max number of bars that be plotted. The default is 25.

• cpos (str, optional) – Color for positives weights. The default is ‘tab:green’.

• cneg (str, optional) – Color for negatives weights. The default is ‘darkorange’.

• cothers (str, optional) – Color for others bar. The default is ‘dodgerblue’.

• height (float, optional) – Height of the image in inches. The default is 10.

• width (float, optional) – Width of the image in inches. The default is 10.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis.

示例

ax = rp.plot_bar(w,
                 title='Portfolio',
                 kind="v",
                 others=0.05,
                 nrow=25,
                 height=6,
                 width=10,
                 ax=None)

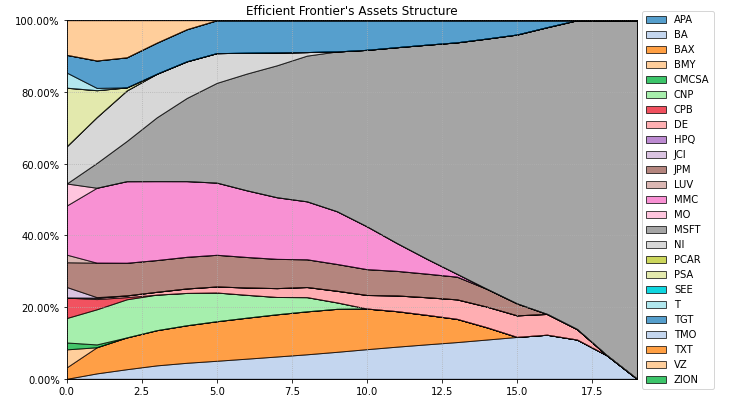
PlotFunctions.plot_frontier_area(w_frontier, nrow=25, cmap='tab20', n_colors=20, height=6, width=10, ax=None)

Create a chart with the asset composition of the efficient frontier.

参数:

• w_frontier (DataFrame) – Weights of portfolios in the efficient frontier.

• nrow (int, optional) – Number of rows of the legend. The default is 25.

• cmap (cmap, optional) – Color scale used to plot each asset weight. The default is ‘tab20’.

• n_colors (int, optional) – Number of distinct colors per color cycle. If there are more assets than n_colors, the chart is going to start to repeat the color cycle. The default is 20.

• height (float, optional) – Height of the image in inches. The default is 6.

• width (float, optional) – Width of the image in inches. The default is 10.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis.

示例

ax = rp.plot_frontier_area(w_frontier=ws,
                           cmap="tab20",
                           height=6,
                           width=10,
                           ax=None)

PlotFunctions.plot_risk_con(w, cov=None, returns=None, rm='MV', rf=0, alpha=0.05, a_sim=100, beta=None, b_sim=None, kappa=0.3, solver=None, percentage=False, erc_line=True, color='tab:blue', erc_linecolor='r', height=6, width=10, t_factor=252, ax=None)

Create a chart with the risk contribution per asset of the portfolio.

参数:

• w (DataFrame of shape (n_assets, 1)) – Portfolio weights.

• cov (DataFrame of shape (n_features, n_features)) – Covariance matrix, where n_features is the number of features.

• returns (DataFrame of shape (n_samples, n_features)) – Features matrix, where n_samples is the number of samples and n_features is the number of features.

• rm (str, optional) –

  Risk measure used to estimate risk contribution. The default is ‘MV’. Possible values are:

  • ’MV’: Standard Deviation.

  • ’KT’: Square Root Kurtosis.

  • ’MAD’: Mean Absolute Deviation.

  • ’GMD’: Gini Mean Difference.

  • ’MSV’: Semi Standard Deviation.

  • ’SKT’: Square Root Semi Kurtosis.

  • ’FLPM’: First Lower Partial Moment (Omega Ratio).

  • ’SLPM’: Second Lower Partial Moment (Sortino Ratio).

  • ’CVaR’: Conditional Value at Risk.

  • ’TG’: Tail Gini.

  • ’EVaR’: Entropic Value at Risk.

  • ’RLVaR’: Relativistic Value at Risk.

  • ’WR’: Worst Realization (Minimax).

  • ’CVRG’: CVaR range of returns.

  • ’TGRG’: Tail Gini range of returns.

  • ’RG’: Range of returns.

  • ’MDD’: Maximum Drawdown of uncompounded cumulative returns (Calmar Ratio).

  • ’ADD’: Average Drawdown of uncompounded cumulative returns.

  • ’CDaR’: Conditional Drawdown at Risk of uncompounded cumulative returns.

  • ’EDaR’: Entropic Drawdown at Risk of uncompounded cumulative returns.

  • ’RLDaR’: Relativistic Drawdown at Risk of uncompounded cumulative returns.

  • ’UCI’: Ulcer Index of uncompounded cumulative returns.

• rf (float, optional) – Risk free rate or minimum acceptable return. The default is 0.

• alpha (float, optional) – Significance level of VaR, CVaR, Tail Gini, EVaR, RLVaR, CDaR, EDaR and RLDaR. The default is 0.05.

• a_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of losses. The default is 100.

• beta (float, optional) – Significance level of CVaR and Tail Gini of gains. If None it duplicates alpha value. The default is None.

• b_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of gains. If None it duplicates a_sim value. The default is None.

• kappa (float, optional) – Deformation parameter of RLVaR and RLDaR, must be between 0 and 1. The default is 0.30.

• solver (str, optional) – Solver available for CVXPY that supports power cone programming. Used to calculate RLVaR and RLDaR. The default value is None.

• percentage (bool, optional) – If risk contribution per asset is expressed as percentage or as a value. The default is False.

• erc_line (bool, optional) – If equal risk contribution line is plotted. The default is False.

• color (str, optional) – Color used to plot each asset risk contribution. The default is ‘tab:blue’.

• erc_linecolor (str, optional) – Color used to plot equal risk contribution line. The default is ‘r’.

• height (float, optional) – Height of the image in inches. The default is 6.

• width (float, optional) – Width of the image in inches. The default is 10.

• t_factor (float, optional) –

  Factor used to annualize expected return and expected risks for risk measures based on returns (not drawdowns). The default is 252.

  \[\begin{split}\begin{align} \text{Annualized Return} & = \text{Return} \, \times \, \text{t_factor} \\ \text{Annualized Risk} & = \text{Risk} \, \times \, \sqrt{\text{t_factor}} \end{align}\end{split}\]

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis.

示例

ax = rp.plot_risk_con(w=w2,
                      cov=cov,
                      returns=returns,
                      rm=rm,
                      rf=0,
                      alpha=0.05,
                      color="tab:blue",
                      height=6,
                      width=10,
                      t_factor=252,
                      ax=None)

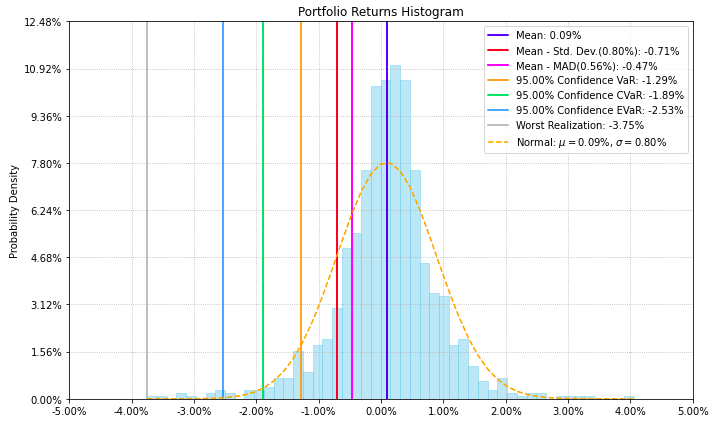
PlotFunctions.plot_hist(returns, w, alpha=0.05, a_sim=100, kappa=0.3, solver=None, bins=50, height=6, width=10, ax=None)

Create a histogram of portfolio returns with the risk measures.

参数:

• returns (DataFrame) – Assets returns.

• w (DataFrame of shape (n_assets, 1)) – Portfolio weights.

• alpha (float, optional) – Significance level of VaR, CVaR, EVaR, RLVaR and Tail Gini. The default is 0.05.

• a_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of losses. The default is 100.

• kappa (float, optional) – Deformation parameter of RLVaR and RLDaR, must be between 0 and 1. The default is 0.30.

• solver (str, optional) – Solver available for CVXPY that supports power cone programming. Used to calculate RLVaR and RLDaR. The default value is None.

• bins (float, optional) – Number of bins of the histogram. The default is 50.

• height (float, optional) – Height of the image in inches. The default is 6.

• width (float, optional) – Width of the image in inches. The default is 10.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis.

示例

ax = rp.plot_hist(returns=Y,
                  w=w1,
                  alpha=0.05,
                  bins=50,
                  height=6,
                  width=10,
                  ax=None)

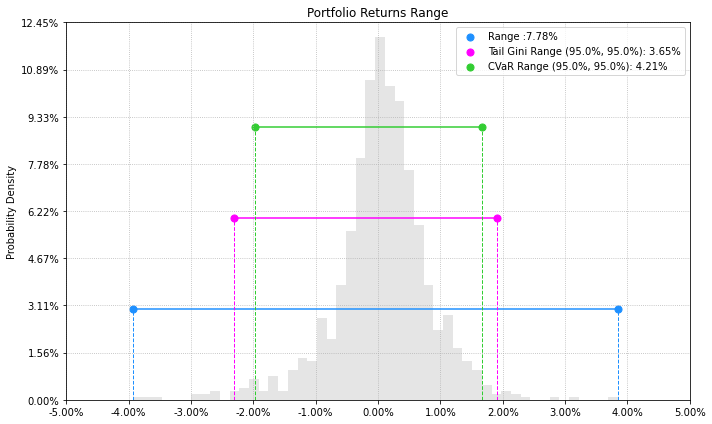
PlotFunctions.plot_range(returns, w, alpha=0.05, a_sim=100, beta=None, b_sim=None, bins=50, height=6, width=10, ax=None)

Create a histogram of portfolio returns with the range risk measures.

参数:

• returns (DataFrame) – Assets returns.

• w (DataFrame of shape (n_assets, 1)) – Portfolio weights.

• alpha (float, optional) – Significance level of CVaR and Tail Gini of losses. The default is 0.05.

• a_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of losses. The default is 100.

• beta (float, optional) – Significance level of CVaR and Tail Gini of gains. If None it duplicates alpha value. The default is None.

• b_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of gains. If None it duplicates a_sim value. The default is None.

• bins (float, optional) – Number of bins of the histogram. The default is 50.

• height (float, optional) – Height of the image in inches. The default is 6.

• width (float, optional) – Width of the image in inches. The default is 10.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis.

示例

ax = plot_range(returns=Y,
                w=w1,
                alpha=0.05,
                a_sim=100,
                beta=None,
                b_sim=None,
                bins=50,
                height=6,
                width=10,
                ax=None)

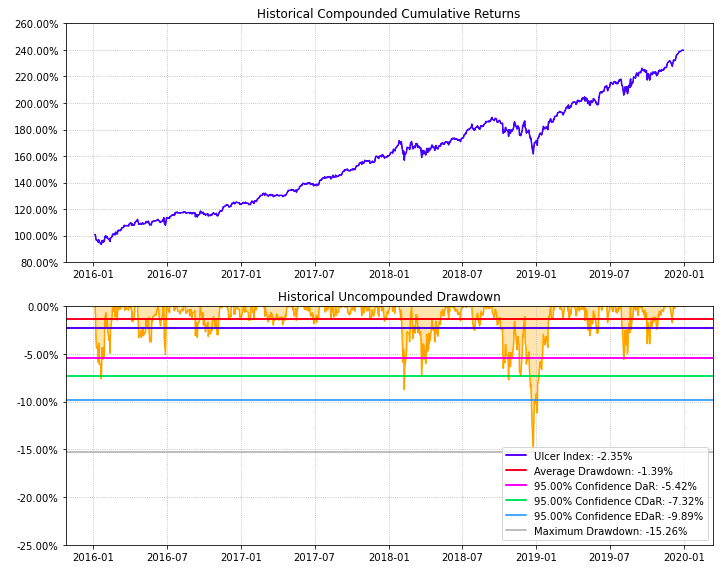
PlotFunctions.plot_drawdown(returns, w, alpha=0.05, kappa=0.3, solver=None, height=8, width=10, height_ratios=[2, 3], ax=None)

Create a chart with the evolution of portfolio prices and drawdown.

参数:

• returns (DataFrame) – Assets returns.

• w (DataFrame, optional) – A portfolio specified by the user. The default is None.

• alpha (float, optional) – Significance level of DaR, CDaR, EDaR and RLDaR. The default is 0.05.

• kappa (float, optional) – Deformation parameter of RLVaR and RLDaR, must be between 0 and 1. The default is 0.30.

• solver (str, optional) – Solver available for CVXPY that supports power cone programming. Used to calculate RLVaR and RLDaR. The default value is None.

• height (float, optional) – Height of the image in inches. The default is 8.

• width (float, optional) – Width of the image in inches. The default is 10.

• height_ratios (list or ndarray) – Defines the relative heights of the rows. Each row gets a relative height of height_ratios[i] / sum(height_ratios). The default value is [2,3].

• ax (matplotlib axis of size (2,1), optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the a np.array with Axes objects with plots for further tweaking.

返回类型:

np.array

示例

ax = rp.plot_drawdown(returns=Y,
                      w=w1,
                      alpha=0.05,
                      height=8,
                      width=10,
                      ax=None)

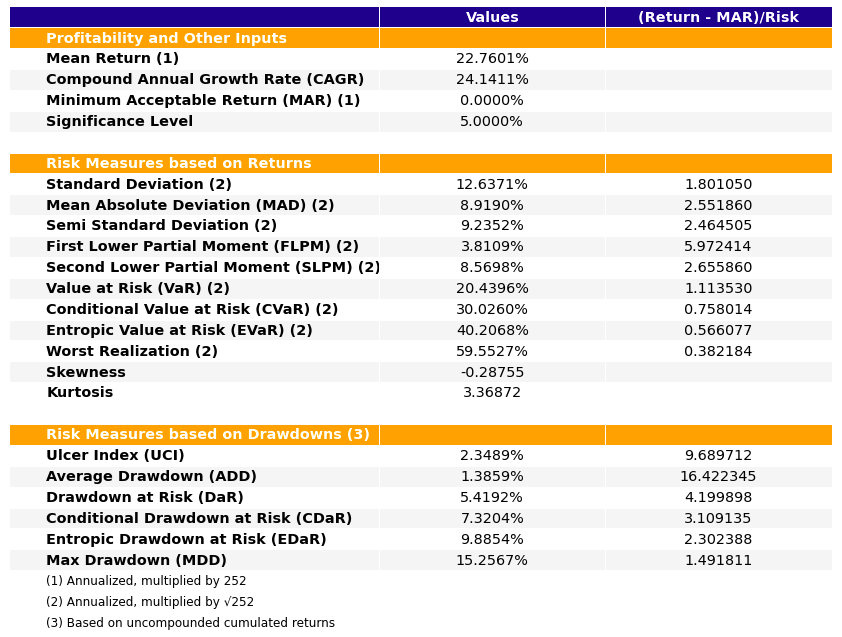
PlotFunctions.plot_table(returns, w, MAR=0, alpha=0.05, a_sim=100, kappa=0.3, solver=None, height=9, width=12, t_factor=252, ini_days=1, days_per_year=252, ax=None)

Create a table with information about risk measures and risk adjusted return ratios.

参数:

• returns (DataFrame) – Assets returns.

• w (DataFrame) – Portfolio weights.

• MAR (float, optional) – Minimum acceptable return.

• alpha (float, optional) – Significance level of VaR, CVaR, Tail Gini, EVaR, RLVaR, CDaR, EDaR and RLDaR. The default is 0.05.

• a_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of losses. The default is 100.

• beta (float, optional) – Significance level of CVaR and Tail Gini of gains. If None it duplicates alpha value. The default is None.

• b_sim (float, optional) – Number of CVaRs used to approximate Tail Gini of gains. If None it duplicates a_sim value. The default is None.

• kappa (float, optional) – Deformation parameter of RLVaR and RLDaR, must be between 0 and 1. The default is 0.30.

• solver (str, optional) – Solver available for CVXPY that supports power cone programming. Used to calculate RLVaR and RLDaR. The default value is None.

• height (float, optional) – Height of the image in inches. The default is 9.

• width (float, optional) – Width of the image in inches. The default is 12.

• t_factor (float, optional) –

  Factor used to annualize expected return and expected risks for risk measures based on returns (not drawdowns). The default is 252.

  \[\begin{split}\begin{align} \text{Annualized Return} & = \text{Return} \, \times \, \text{t_factor} \\ \text{Annualized Risk} & = \text{Risk} \, \times \, \sqrt{\text{t_factor}} \end{align}\end{split}\]

• ini_days (float, optional) – If provided, it is the number of days of compounding for first return. It is used to calculate Compound Annual Growth Rate (CAGR). This value depend on assumptions used in t_factor, for example if data is monthly you can use 21 (252 days per year) or 30 (360 days per year). The default is 1 for daily returns.

• days_per_year (float, optional) – Days per year assumption. It is used to calculate Compound Annual Growth Rate (CAGR). Default value is 252 trading days per year.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis

示例

ax = rp.plot_table(returns=Y,
                   w=w1,
                   MAR=0,
                   alpha=0.05,
                   ax=None)

PlotFunctions.plot_clusters(returns, custom_cov=None, codependence='pearson', linkage='ward', k=None, max_k=10, bins_info='KN', alpha_tail=0.05, gs_threshold=0.5, leaf_order=True, show_clusters=True, dendrogram=True, cmap='RdYlBu', linecolor='fuchsia', title='', height=12, width=12, ax=None)

Create a clustermap plot based on the selected codependence measure.

参数:

• returns (DataFrame) – Assets returns.

• custom_cov (DataFrame or None, optional) – Custom covariance matrix, used when codependence parameter has value ‘custom_cov’. The default is None.

• codependence (str, can be {'pearson', 'spearman', 'abs_pearson', 'abs_spearman', 'distance', 'mutual_info', 'tail' or 'custom_cov'}) –

  The codependence or similarity matrix used to build the distance metric and clusters. The default is ‘pearson’. Possible values are:

  • ’pearson’: pearson correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho_{i,j})}\).

  • ’spearman’: spearman correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho_{i,j})}\).

  • ’kendall’: kendall correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{kendall}_{i,j})}\).

  • ’gerber1’: Gerber statistic 1 correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{gerber1}_{i,j})}\).

  • ’gerber2’: Gerber statistic 2 correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{gerber2}_{i,j})}\).

  • ’abs_pearson’: absolute value pearson correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’abs_spearman’: absolute value spearman correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’abs_kendall’: absolute value kendall correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho^{kendall}_{i,j}|)}\).

  • ’distance’: distance correlation matrix. Distance formula \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’mutual_info’: mutual information matrix. Distance used is variation information matrix.

  • ’tail’: lower tail dependence index matrix. Dissimilarity formula \(D_{i,j} = -\log{\lambda_{i,j}}\).

  • ’custom_cov’: use custom correlation matrix based on the custom_cov parameter. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{pearson}_{i,j})}\).

• linkage (string, optional) –

  Linkage method of hierarchical clustering, see linkage for more details. The default is ‘ward’. Possible values are:

  • ’single’.

  • ’complete’.

  • ’average’.

  • ’weighted’.

  • ’centroid’.

  • ’median’.

  • ’ward’.

  • ’DBHT’: Direct Bubble Hierarchical Tree.

• k (int, optional) – Number of clusters. This value is took instead of the optimal number of clusters calculated with the two difference gap statistic. The default is None.

• max_k (int, optional) – Max number of clusters used by the two difference gap statistic to find the optimal number of clusters. The default is 10.

• bins_info (int or str) –

  Number of bins used to calculate variation of information. The default value is ‘KN’. Possible values are:

  • ’KN’: Knuth’s choice method. See more in knuth_bin_width.

  • ’FD’: Freedman–Diaconis’ choice method. See more in freedman_bin_width.

  • ’SC’: Scotts’ choice method. See more in scott_bin_width.

  • ’HGR’: Hacine-Gharbi and Ravier’ choice method.

  • int: integer value choice by user.

• alpha_tail (float, optional) – Significance level for lower tail dependence index. The default is 0.05.

• gs_threshold (float, optional) – Gerber statistic threshold. The default is 0.5.

• leaf_order (bool, optional) – Indicates if the cluster are ordered so that the distance between successive leaves is minimal. The default is True.

• show_clusters (bool, optional) – Indicates if clusters are plot. The default is True.

• dendrogram (bool, optional) – Indicates if the plot has or not a dendrogram. The default is True.

• cmap (str or cmap, optional) – Colormap used to plot the pcolormesh plot. The default is ‘viridis’.

• linecolor (str, optional) – Color used to identify the clusters in the pcolormesh plot. The default is fuchsia’.

• title (str, optional) – Title of the chart. The default is “”.

• height (float, optional) – Height of the image in inches. The default is 12.

• width (float, optional) – Width of the image in inches. The default is 12.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis

示例

ax = rp.plot_clusters(returns=Y,
                      codependence='spearman',
                      linkage='ward',
                      k=None,
                      max_k=10,
                      leaf_order=True,
                      dendrogram=True,
                      ax=None)

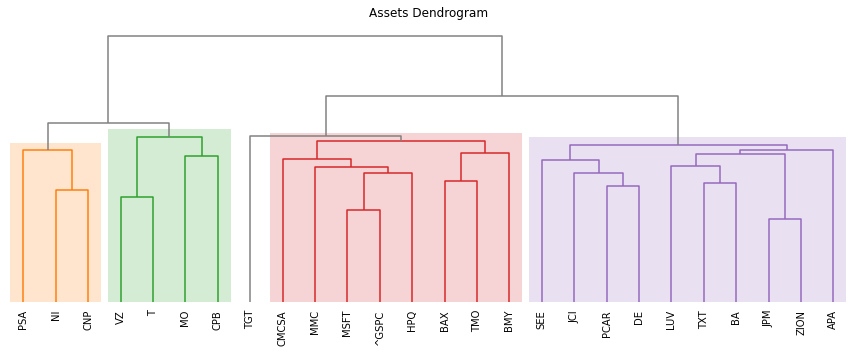
PlotFunctions.plot_dendrogram(returns, custom_cov=None, codependence='pearson', linkage='ward', k=None, max_k=10, bins_info='KN', alpha_tail=0.05, gs_threshold=0.5, leaf_order=True, show_clusters=True, title='', height=5, width=12, ax=None)

Create a dendrogram based on the selected codependence measure.

参数:

• returns (DataFrame) – Assets returns.

• custom_cov (DataFrame or None, optional) – Custom covariance matrix, used when codependence parameter has value ‘custom_cov’. The default is None.

• codependence (str, can be {'pearson', 'spearman', 'abs_pearson', 'abs_spearman', 'distance', 'mutual_info', 'tail' or 'custom_cov'}) –

  The codependence or similarity matrix used to build the distance metric and clusters. The default is ‘pearson’. Possible values are:

  • ’pearson’: pearson correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho_{i,j})}\).

  • ’spearman’: spearman correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho_{i,j})}\).

  • ’kendall’: kendall correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{kendall}_{i,j})}\).

  • ’gerber1’: Gerber statistic 1 correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{gerber1}_{i,j})}\).

  • ’gerber2’: Gerber statistic 2 correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{gerber2}_{i,j})}\).

  • ’abs_pearson’: absolute value pearson correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’abs_spearman’: absolute value spearman correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’abs_kendall’: absolute value kendall correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho^{kendall}_{i,j}|)}\).

  • ’distance’: distance correlation matrix. Distance formula \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’mutual_info’: mutual information matrix. Distance used is variation information matrix.

  • ’tail’: lower tail dependence index matrix. Dissimilarity formula \(D_{i,j} = -\log{\lambda_{i,j}}\).

  • ’custom_cov’: use custom correlation matrix based on the custom_cov parameter. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{pearson}_{i,j})}\).

• linkage (string, optional) –

  Linkage method of hierarchical clustering, see linkage for more details. The default is ‘ward’. Possible values are:

  • ’single’.

  • ’complete’.

  • ’average’.

  • ’weighted’.

  • ’centroid’.

  • ’median’.

  • ’ward’.

  • ’DBHT’: Direct Bubble Hierarchical Tree.

• k (int, optional) – Number of clusters. This value is took instead of the optimal number of clusters calculated with the two difference gap statistic. The default is None.

• max_k (int, optional) – Max number of clusters used by the two difference gap statistic to find the optimal number of clusters. The default is 10.

• bins_info (int or str) –

  Number of bins used to calculate variation of information. The default value is ‘KN’. Possible values are:

  • ’KN’: Knuth’s choice method. See more in knuth_bin_width.

  • ’FD’: Freedman–Diaconis’ choice method. See more in freedman_bin_width.

  • ’SC’: Scotts’ choice method. See more in scott_bin_width.

  • ’HGR’: Hacine-Gharbi and Ravier’ choice method.

  • int: integer value choice by user.

• alpha_tail (float, optional) – Significance level for lower tail dependence index. The default is 0.05.

• gs_threshold (float, optional) – Gerber statistic threshold. The default is 0.5.

• leaf_order (bool, optional) – Indicates if the cluster are ordered so that the distance between successive leaves is minimal. The default is True.

• show_clusters (bool, optional) – Indicates if clusters are plot. The default is True.

• title (str, optional) – Title of the chart. The default is “”.

• height (float, optional) – Height of the image in inches. The default is 5.

• width (float, optional) – Width of the image in inches. The default is 12.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis

示例

ax = rp.plot_dendrogram(returns=Y,
                        codependence='spearman',
                        linkage='ward',
                        k=None,
                        max_k=10,
                        leaf_order=True,
                        ax=None)

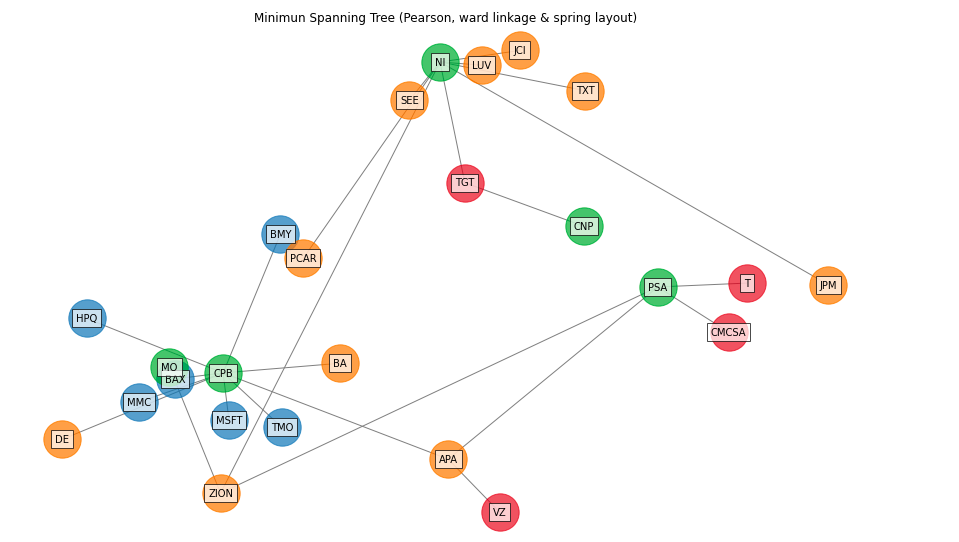
PlotFunctions.plot_network(returns, custom_cov=None, codependence='pearson', linkage='ward', k=None, max_k=10, bins_info='KN', alpha_tail=0.05, gs_threshold=0.5, leaf_order=True, kind='spring', seed=0, node_labels=True, node_size=1400, node_alpha=0.7, font_size=10, title='', height=8, width=10, ax=None)

Create a network plot. The Planar Maximally Filtered Graph (PMFG) for DBHT linkage and Minimum Spanning Tree (MST) for other linkage methods.

参数:

• returns (DataFrame) – Assets returns.

• custom_cov (DataFrame or None, optional) – Custom covariance matrix, used when codependence parameter has value ‘custom_cov’. The default is None.

• codependence (str, can be {'pearson', 'spearman', 'abs_pearson', 'abs_spearman', 'distance', 'mutual_info', 'tail' or 'custom_cov'}) –

  The codependence or similarity matrix used to build the distance metric and clusters. The default is ‘pearson’. Possible values are:

  • ’pearson’: pearson correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{pearson}_{i,j})}\).

  • ’spearman’: spearman correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{spearman}_{i,j})}\).

  • ’kendall’: kendall correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{kendall}_{i,j})}\).

  • ’gerber1’: Gerber statistic 1 correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{gerber1}_{i,j})}\).

  • ’gerber2’: Gerber statistic 2 correlation matrix. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{gerber2}_{i,j})}\).

  • ’abs_pearson’: absolute value pearson correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’abs_spearman’: absolute value spearman correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho_{i,j}|)}\).

  • ’abs_kendall’: absolute value kendall correlation matrix. Distance formula: \(D_{i,j} = \sqrt{(1-|\rho^{kendall}_{i,j}|)}\).

  • ’distance’: distance correlation matrix. Distance formula \(D_{i,j} = \sqrt{(1-\rho^{distance}_{i,j})}\).

  • ’mutual_info’: mutual information matrix. Distance used is variation information matrix.

  • ’tail’: lower tail dependence index matrix. Dissimilarity formula \(D_{i,j} = -\log{\lambda_{i,j}}\).

  • ’custom_cov’: use custom correlation matrix based on the custom_cov parameter. Distance formula: \(D_{i,j} = \sqrt{0.5(1-\rho^{pearson}_{i,j})}\).

• linkage (string, optional) –

  Linkage method of hierarchical clustering, see linkage for more details. The default is ‘ward’. Possible values are:

  • ’single’.

  • ’complete’.

  • ’average’.

  • ’weighted’.

  • ’centroid’.

  • ’median’.

  • ’ward’.

  • ’DBHT’: Direct Bubble Hierarchical Tree.

• k (int, optional) – Number of clusters. This value is took instead of the optimal number of clusters calculated with the two difference gap statistic. The default is None.

• max_k (int, optional) – Max number of clusters used by the two difference gap statistic to find the optimal number of clusters. The default is 10.

• bins_info (int or str) –

  Number of bins used to calculate variation of information. The default value is ‘KN’. Possible values are:

  • ’KN’: Knuth’s choice method. See more in knuth_bin_width.

  • ’FD’: Freedman–Diaconis’ choice method. See more in freedman_bin_width.

  • ’SC’: Scotts’ choice method. See more in scott_bin_width.

  • ’HGR’: Hacine-Gharbi and Ravier’ choice method.

  • int: integer value choice by user.

• alpha_tail (float, optional) – Significance level for lower tail dependence index. The default is 0.05.

• gs_threshold (float, optional) – Gerber statistic threshold. The default is 0.5.

• leaf_order (bool, optional) – Indicates if the cluster are ordered so that the distance between successive leaves is minimal. The default is True.

• kind (str, optional) –

  Kind of networkx layout. The default value is ‘spring’. Possible values are:

  • ’spring’: networkx spring_layout.

  • ’planar’. networkx planar_layout.

  • ’circular’. networkx circular_layout.

  • ’kamada’. networkx kamada_kawai_layout. Only available for positive codependence metrics. Not pearson or spearman except when linkage is DBHT.

• seed (int, optional) – Seed for networkx spring layout. The default value is 0.

• node_labels (bool, optional) – Specify if node lables are visible. The default value is True.

• node_size (float, optional) – Size of the nodes. The default value is 1600.

• node_alpha (float, optional) – Alpha parameter or transparency of nodes. The default value is 0.7.

• font_size (float, optional) – Font size of node labels. The default value is 12.

• title (str, optional) – Title of the chart. The default is “”.

• height (float, optional) – Height of the image in inches. The default is 5.

• width (float, optional) – Width of the image in inches. The default is 12.

• ax (matplotlib axis, optional) – If provided, plot on this axis. The default is None.

抛出:

ValueError – When the value cannot be calculated.

返回:

ax – Returns the Axes object with the plot for further tweaking.

返回类型:

matplotlib axis

示例

ax = rp.plot_network(returns=Y,
                     codependence="pearson",
                     linkage="ward",
                     k=None,
                     max_k=10,
                     alpha_tail=0.05,
                     leaf_order=True,
                     kind='spring',
                     ax=None)