什么是CVXPY？

CVXPY是一个Python嵌入建模语言，用于凸优化问题。它会自动将问题转换为标准形式，调用求解器并解包结果。

下面的代码使用CVXPY解决了一个简单的优化问题：

import cvxpy as cp

# 创建两个标量优化变量。
x = cp.Variable()
y = cp.Variable()

# 创建两个约束条件。
constraints = [x + y == 1,
               x - y >= 1]

# 构建目标函数。
obj = cp.Minimize((x - y)**2)

# 构建并求解问题。
prob = cp.Problem(obj, constraints)
prob.solve()  # 返回最优值。
print("status:", prob.status)
print("optimal value", prob.value)
print("optimal var", x.value, y.value)

状态：最优
最优值：0.999999999761
最优解：1.00000000001 -1.19961841702e-11

“optimal”是通过solve方法分配给状态的值，告诉我们问题已成功解决。最优值（在这里基本上是1）是在满足约束条件的所有变量选择中，目标的最小值。最后一行打印出了实现最佳目标的x和y的值（基本上是1和0）。

prob.solve() 返回最优值并更新 prob.status ， prob.value 和问题中所有变量的 value 字段。

更改问题

Problems 是不可变的，这意味着它们在创建后不能更改。要更改目标或约束，请创建一个新问题。

# 替换目标。
prob2 = cp.Problem(cp.Maximize(x + y), prob.constraints)
print("optimal value", prob2.solve())

# 替换约束条件（x + y == 1）。
constraints = [x + y <= 3] + prob2.constraints[1:]
prob3 = cp.Problem(prob2.objective, constraints)
print("optimal value", prob3.solve())

optimal value 1.0
optimal value 3.00000000006

不可行和无界问题

如果问题不可行或无界，状态字段将被设置为“不可行”或“无界”。问题变量的值字段不会被更新。

import cvxpy as cp

x = cp.Variable()

# 一个不可行的问题。
prob = cp.Problem(cp.Minimize(x), [x >= 1, x <= 0])
prob.solve()
print("status:", prob.status)
print("optimal value", prob.value)

# 一个无界问题。
prob = cp.Problem(cp.Minimize(x))
prob.solve()
print("status:", prob.status)
print("optimal value", prob.value)

status: infeasible
optimal value inf
status: unbounded
optimal value -inf

请注意，对于最小化问题，如果问题无法实现，则最优值为 inf ；如果问题无界，则最优值为 -inf 。对于最大化问题来说，情况正好相反。

其他问题状态

如果CVXPY调用的求解器解决了问题，但精度较低，问题状态将指示达到的较低精度。表示较低精度的状态有：

• “optimal_inaccurate”

• “unbounded_inaccurate”

• “infeasible_inaccurate”

对于找到的解类型（即最优解、无界解或无可行解），问题变量会按照通常的方式进行更新。

如果求解器完全无法解决问题，CVXPY会抛出 SolverError 异常。如果发生这种情况，您应该尝试使用其他求解器。有关详细信息，请参阅 选择求解器 讨论。

CVXPY为不同状态字符串提供以下常量别名：

• OPTIMAL

• INFEASIBLE

• UNBOUNDED

• OPTIMAL_INACCURATE

• INFEASIBLE_INACCURATE

• UNBOUNDED_INACCURATE

• INFEASIBLE_OR_UNBOUNDED

要测试问题是否成功解决，您应该使用以下代码:

prob.status == OPTIMAL

INFEASIBLE_OR_UNBOUNDED 状态很少见。它用于当求解器能够确定问题是不可行的还是无界的，但不能确定具体是哪个情况。您可以通过将目标函数设置为一个常数（例如， objective = cp.Minimize(0) ）来确定确切的状态。如果使用状态码 INFEASIBLE_OR_UNBOUNDED 解决了新问题，则原始问题是不可行的。如果新问题使用状态 OPTIMAL 解决，则原始问题是无界的。

向量和矩阵

Variables 可以是标量、向量或矩阵，即它们可以是 0、1 或 2 维的。

# 标量变量。
a = cp.Variable()

# 形状为 (5,) 的向量变量。
x = cp.Variable(5)

# 形状为 (5, 1) 的矩阵变量。
x = cp.Variable((5, 1))

# 形状为 (4, 7) 的矩阵变量。
A = cp.Variable((4, 7))

您可以使用您选择的数值库构造矩阵和向量常量。例如，如果 x 是 CVXPY 表达式 A @ x + b 中的变量，那么 A 和 b 可以是 Numpy 数组、SciPy 稀疏矩阵等。甚至 A 和 b 可以是不同类型的。

目前可以使用以下类型作为常数：

• NumPy的ndarrays（NumPy的多维数组）

• NumPy的matrices（NumPy的矩阵）

• SciPy的sparse matrices（SciPy的稀疏矩阵）

下面是一个使用向量和矩阵的CVXPY问题的示例：

# 求解有界最小二乘问题。

import cvxpy as cp
import numpy

# 问题数据。
m = 10
n = 5
numpy.random.seed(1)
A = numpy.random.randn(m, n)
b = numpy.random.randn(m)

# 构建问题。
x = cp.Variable(n)
objective = cp.Minimize(cp.sum_squares(A @ x - b))
constraints = [0 <= x, x <= 1]
prob = cp.Problem(objective, constraints)

print("Optimal value", prob.solve())
print("Optimal var")
print(x.value) # 一个NumPy的ndarray。

  最优值为 4.14133859146
  最优变量
  [ -5.11480673e-21   6.30625742e-21   1.34643668e-01   1.24976681e-01
-4.79039542e-21]

约束条件

如示例代码所示，您可以使用 == ， <= 和 >= 来构建CVXPY中的约束条件。等式约束和不等式约束在标量、向量或矩阵中都是逐元素处理的。例如，约束条件 0 <= x 和 x <= 1 意味着 x 的每个元素都介于0和1之间。

如果要表示半定锥约束的矩阵不等式，请参见 semidefinite 。该部分详细说明了如何表达半定锥不等式。

您不能使用 < 和 > 构建不等式。在现实世界中，严格不等式是没有意义的。此外，您不能将约束链在一起，例如 0 <= x <= 1 或 x == y == 2 。Python解释器会以CVXPY无法捕获的方式处理链式约束。如果您编写了链式约束，CVXPY将引发异常。

参数

Parameters 是常量的符号表示。参数的目的是在不重构整个问题的情况下更改问题中常量的值。在许多情况下，多次求解参数化程序比重复求解新问题要快得多：阅读本节后，请务必阅读关于 纪律化参数化编程 （DPP）的教程。

参数可以是向量或矩阵，就像变量一样。创建参数时，您有选项可以指定参数条目的属性，例如参数条目的符号，参数是否对称等。这些属性在 标准凸规划 中使用，并且在未指定时是未知的。参数可以在创建后的任何时候被赋予一个常量值。常量值必须具有与创建参数时指定的维度和属性相同。

# 正数标量参数。
m = cp.Parameter(nonneg=True)

# 具有未知符号的列向量参数（默认情况下）。
c = cp.Parameter(5)

# 具有负数条目的矩阵参数。
G = cp.Parameter((4, 7), nonpos=True)

# 将常量值赋给G。
G.value = -numpy.ones((4, 7))

可以使用一个值来初始化参数。下面的代码段是等价的:

# 创建参数，然后赋值。
rho = cp.Parameter(nonneg=True)
rho.value = 2

# 使用一个值来初始化参数。
rho = cp.Parameter(nonneg=True, value=2)

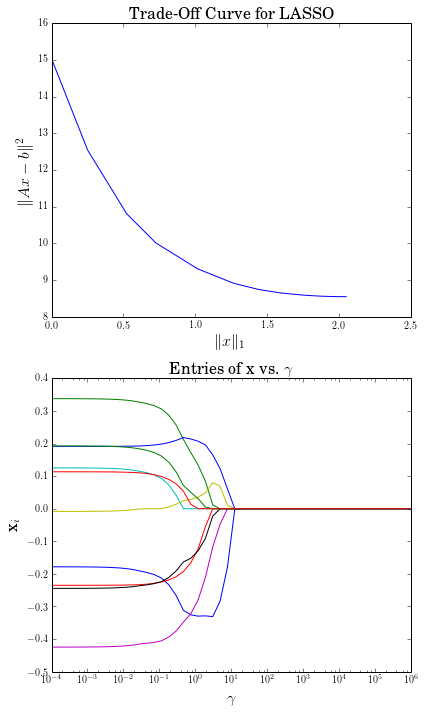
计算权衡曲线是参数的常见用法。下面的示例计算一个LASSO问题的权衡曲线。

import cvxpy as cp
import numpy
import matplotlib.pyplot as plt

# 问题数据。
n = 15
m = 10
numpy.random.seed(1)
A = numpy.random.randn(n, m)
b = numpy.random.randn(n)
# 由于DCP规则，gamma必须是非负的。
gamma = cp.Parameter(nonneg=True)

# 构造问题。
x = cp.Variable(m)
error = cp.sum_squares(A @ x - b)
obj = cp.Minimize(error + gamma*cp.norm(x, 1))
prob = cp.Problem(obj)

# 构造 ||Ax-b||^2 vs. ||x||_1 的权衡曲线
sq_penalty = []
l1_penalty = []
x_values = []
gamma_vals = numpy.logspace(-4, 6)
for val in gamma_vals:
    gamma.value = val
    prob.solve()
    # 使用expr.value获取问题中表达式的数值。
    sq_penalty.append(error.value)
    l1_penalty.append(cp.norm(x, 1).value)
    x_values.append(x.value)

plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.figure(figsize=(6,10))

# 绘制权衡曲线。
plt.subplot(211)
plt.plot(l1_penalty, sq_penalty)
plt.xlabel(r'\|x\|_1', fontsize=16)
plt.ylabel(r'\|Ax-b\|^2', fontsize=16)
plt.title('Trade-Off Curve for LASSO', fontsize=16)

# 绘制x的条目 vs. gamma。
plt.subplot(212)
for i in range(m):
    plt.plot(gamma_vals, [xi[i] for xi in x_values])
plt.xlabel(r'\gamma', fontsize=16)
plt.ylabel(r'x_{i}', fontsize=16)
plt.xscale('log')
plt.title(r'\text{Entries of x vs. }\gamma', fontsize=16)

plt.tight_layout()
plt.show()

可以轻松地并行计算权衡曲线。下面的代码在并行计算上述LASSO问题中每个 \(\gamma\) 的最优x。

from multiprocessing import Pool

# 为 gamma 赋值并找到最优的 x。
def get_x(gamma_value):
    gamma.value = gamma_value
    result = prob.solve()
    return x.value

# 并行计算（此处设置为 1 个进程）。
pool = Pool(processes = 1)
x_values = pool.map(get_x, gamma_vals)