高级特性

本教程的本节介绍了CVXPY的高级凸优化特性，适用于具有高级凸优化知识的用户。我们建议参考 `Convex Optimization`_ 一书（作者：Boyd和Vandenberghe），以了解您不熟悉的任何术语。

对偶变量

您可以使用CVXPY找到问题的最优对偶变量。当您调用 prob.solve() 时，解决方案中的每个对偶变量都存储在其对应约束的 dual_value 字段中。

import cvxpy as cp

# 创建两个标量优化变量。
x = cp.Variable()
y = cp.Variable()

# 创建两个约束。
constraints = [x + y == 1,
               x - y >= 1]

# 构建目标函数。
obj = cp.Minimize((x - y)**2)# 形成和解决问题。
prob = cp.Problem(obj, constraints)
prob.solve()

# 约束条件的最优对偶变量（拉格朗日乘子）存储在 constraint.dual_value 中。
print("最优的 (x + y == 1) 对偶变量：", constraints[0].dual_value)
print("最优的 (x - y >= 1) 对偶变量：", constraints[1].dual_value)
print("x - y 的值：", (x - y).value)

最优的 (x + y == 1) 对偶变量：6.47610300459e-18
最优的 (x - y >= 1) 对偶变量：2.00025244976
x - y 的值：0.999999986374

对于 x - y >= 1 的对偶变量为 2. 根据互补性，这意味着 x - y 的值为 1，我们可以看到这是正确的。对偶变量非零还告诉我们，如果我们加强约束条件 x - y >= 1 （即增加右侧），问题的最优值将会增加。

属性

可以使用属性来创建变量和参数，以指定额外的属性。例如，Variable(nonneg=True) 是一个标量变量，受到非负约束。类似地，Parameter(nonpos=True) 是一个标量参数，受到非正约束。Leaf 的完整构造函数（即 Variable 和 Parameter 的父类）如下所示。

Leaf(shape=None, value=None, nonneg=False, nonpos=False, complex=False, imag=False, symmetric=False, diag=False, PSD=False, NSD=False, hermitian=False, boolean=False, integer=False, sparsity=None, pos=False, neg=False)

创建一个 Leaf 对象（例如 Variable 或 Parameter）。 只能有一个属性处于活动状态（设置为 True）。

Parameters:

• shape (元组或整数) – 变量的维度（默认为0D）。不能超过2D。

• value (数值类型) – 要分配给变量的值。

• nonneg (布尔类型) – 变量是否受非负约束？

• nonpos (布尔类型) – 变量是否受非正约束？

• complex (布尔类型) – 变量是否受复数值约束？

• imag (布尔类型) – 变量是否受虚数约束？

• symmetric (布尔类型) – 变量是否受对称约束？

• diag (布尔类型) – 变量是否受对角线约束？

• PSD (布尔类型) – 变量是否受对称正半定约束？

• NSD (布尔类型) – 变量是否受对称负半定约束？

• hermitian (布尔类型) – 变量是否受Hermitian约束？

• boolean (布尔类型或元组列表) – 变量是否为布尔型（即为0或1）？True表示整个变量受布尔约束，False表示不受约束，或者为应受布尔约束的索引列表，其中每个索引是长度与shape长度相等的元组。

• integer (布尔类型或元组列表) – 变量是否为整数？语义与boolean参数相同。

• sparsity (元组列表) – 变量的固定稀疏模式。

• pos (布尔类型) – 变量是否受正约束？

• neg (布尔类型) – 变量是否受负约束？

Variables和Parameters的 value 字段可以在构建后分配一个值，但分配的值必须满足对象的属性。 根据属性定义的集合上的欧几里得投影由 project 方法给出。

p = Parameter(nonneg=True)
try:
    p.value = -1
except Exception as e:
    print(e)

print("Projection:", p.project(-1))

Parameter value must be nonnegative.
Projection: 0.0

给叶子节点分配值的一个合理的习语是 leaf.value = leaf.project(val)， 确保分配的值满足叶子节点的属性。一个稍微更高效的变体是 leaf.project_and_assign(val)， 它直接进行投影和赋值，而不需要额外检查值是否满足叶子节点的属性。在大多数情况下，project 和检查值是否满足叶子节点的属性是廉价的操作（即 \(O(n)\)）， 但对于对称正半定或负半定叶子节点，这些操作会计算特征值分解。

许多属性，如非负性和对称性，可以用约束很容易地指定。 那么，在变量中指定属性的优势是什么呢？ 主要的好处是指定属性能够实现更精细的DCP分析。 例如，通过 x = Variable(nonpos=True) 创建变量 x，可以在DCP分析器中提供 x 非正的信息。 通过使用 x = Variable() 创建变量 x，然后单独添加约束 x >= 0，则对DCP分析器不提供有关 x 符号的任何信息。

使用属性而不是显式约束的一个缺点是，不会记录对偶变量。对偶变量值仅适用于显式约束。.. _semidefinite:

半定矩阵

许多凸优化问题涉及将矩阵约束为正定或负定（例如，SDP问题）。 在CVXPY中，有两种方法可以实现这一点。 第一种方法是使用``Variable((n, n), PSD=True)``来创建一个对称且正定的``n``行``n``列的变量。例如,

# 创建一个100x100的正定变量。
X = cp.Variable((100, 100), PSD=True)

# 在任何您使用CVXPY变量的地方，都可以使用X。
obj = cp.Minimize(cp.norm(X) + cp.sum(X))

第二种方法是使用``>>``或``<<``操作符创建一个正定锥约束。 如果``X``和``Y``是``n``行``n``列的变量， 约束``X >> Y``意味着对于所有的:math:z in mathcal{R}^n，都满足 \(z^T(X - Y)z \geq 0\)。 换句话说，:math:`(X - Y) + (X - Y)^T`是正定的。 该约束不要求``X``和``Y``是对称的。 正定锥约束的两侧必须都是方阵且是仿射的。

下面的代码演示了如何将矩阵表达式约束为正定或负定（但不一定是对称的）。

# expr1必须是正定的。
constr1 = (expr1 >> 0)

# expr2 必须为半负定的。
constr2 = (expr2 << 0)

为了将矩阵表达式限制为对称的，只需写如下：

# expr 必须为对称的。
constr = (expr == expr.T)

您还可以使用 Variable((n, n), symmetric=True) 创建一个 n 行 n 列的变量，并约束其为对称的。 通过在属性中指定变量为对称的和添加约束 X == X.T 之间的区别在于， 属性会被解析为 DCP 信息，并将对称变量定义在对称矩阵的（较低维度的）向量空间上。

混合整数规划

在混合整数规划中，某些变量被限制为布尔值（即0或1）或整数值。 您可以通过创建属性为只有布尔值或整数值的变量来构建混合整数规划：

# 创建一个由10个布尔值组成的向量。
x = cp.Variable(10, boolean=True)

# expr1 必须是布尔值。
constr1 = (expr1 == x)

# 创建一个5行7列的矩阵，其值受限于整数。
Z = cp.Variable((5, 7), integer=True)

# expr2 必须是整数值。
constr2 = (expr2 == Z)

CVXPY提供了许多混合整数求解器的接口，包括开源和商业求解器。 出于许可原因，CVXPY默认不安装任何首选求解器。

CVXPY中首选的开源混合整数求解器是GLPK_MI_，CBC_和SCIP_。CVXOPT Python包提供了CVXPY访问GLPK_MI的功能；可以通过在命令行或终端中运行 ``pip install cvxopt``来安装CVXOPT。SCIP支持非线性模型，但 GLPK_MI和CBC不支持。

CVXPY默认附带了一个名为ECOS_BB的开源混合整数非线性求解器。然而， 不会自动调用ECOS_BB；如果要使用它，必须显式调用 prob.solve(solver='ECOS_BB') ( CVXPY 1.1.6中的更改 )。这样做的原因是 ECOS_BB存在一些频繁的正确性问题。如果您依赖于此求解器用于某些 应用程序，则需要注意使用它所带来的增加的风险。 如果您需要使用CVXPY中的开源混合整数非线性求解器， 我们建议您安装SCIP。

如果您需要快速求解一个大型混合整数问题，或者您有一个对SCIP来说具有挑战性的非线性混合整数 模型，那么您将需要使用像CPLEX_，GUROBI，XPRESS，MOSEK_或COPT_这样的商业求解器。运行商业求解器需要许可证。 CPLEX，GUROBI和MOSEK向学术界（包括学生和教师）提供免费许可证，并向学术界以外的人提供试用版。 CPLEX Free Edition可以无需付费获得，无论学术身份如何，但仍需要 在线注册，仅限于最多1000个变量和1000个约束的问题。 XPRESS有一个免费社区版，不需要注册，但限制 变量数量和约束数量之和不超过5000的问题。 COPT还有一个免费社区版，限制变量数量和约束数量最多为2000。

Note

如果您开发了一个遵循Apache 2.0等宽松许可证的开源混合整数求解器， 并且您有兴趣将您的求解器合并到CVXPY的默认安装中，请通过 GitHub issues 与我们联系。我们非常 有兴趣将简单的混合整数SOCP求解器合并到CVXPY中。

复数表达式

默认情况下，变量和参数的值是实数。 可以通过设置属性 complex=True 来创建复数变量和参数。 同样，可以通过设置属性 imag=True 来创建纯虚数变量和参数。 包含复数变量、参数或常数的表达式可能是复数值。 函数 is_real ， is_complex 和 is_imag 分别返回表达式是否是纯实数、复数或纯虚数。

# 一个复数变量。
x = cp.Variable(complex=True)
# 一个纯虚数参数。
p = cp.Parameter(imag=True)

print("p.is_imag() = ", p.is_imag())
print("(x + 2).is_real() = ", (x + 2).is_real())

p.is_imag() = True
(x + 2).is_real() = False

问题目标中的顶级表达式必须是实数值的，但子表达式可以是复数的。 对于复数表达式，可以定义算术和所有线性原子。 对于复数表达式，额外定义了非线性原子 abs 和所有范数，除了 norm(X, p) 其中 p < 1。 对称矩阵域的所有原子对于厄米矩阵都有定义。 类似地，对于复数 x 和厄米矩阵 P，定义了原子 quad_form(x, P) 和 matrix_frac(x, P)。 对于复数表达式，所有约束都有定义。

提供了以下用于处理复数表达式的其他原子：

• real(expr) 计算 expr 的实部。

• imag(expr) 计算 expr 的虚部（即，expr = real(expr) + 1j*imag(expr)）。

• conj(expr) 计算 expr 的复共轭。

• expr.H 计算 expr 的厄米（共轭转置）。

变换

变换提供了在原子函数之外进一步操作CVXPY对象的方式。例如，indicator 变换将一组约束转换为表示当约束满足时取值为0，约束违反时取值为 \(\infty\) 的凸函数表达式。

x = cp.Variable()
constraints = [0 <= x, x <= 1]
expr = cp.transforms.indicator(constraints)
x.value = .5
print("expr.value = ", expr.value)
x.value = 2
print("expr.value = ", expr.value)

expr.value = 0.0
expr.value = inf

可用的全部转换在 转换 中讨论。

问题数学运算

为方便起见，已经对问题和目标函数进行了重载。 问题数学运算很有用，因为它允许将一个问题写成小问题的总和。 下面给出了目标函数相加、相减和相乘的规则。

# 加法和减法。

Minimize(expr1) + Minimize(expr2) == Minimize(expr1 + expr2)

Maximize(expr1) + Maximize(expr2) == Maximize(expr1 + expr2)

Minimize(expr1) + Maximize(expr2) # Not allowed.

Minimize(expr1) - Maximize(expr2) == Minimize(expr1 - expr2)

# 乘法（alpha 是一个正标量）

alpha*Minimize(expr) == Minimize(alpha*expr)

alpha*Maximize(expr) == Maximize(alpha*expr)

-alpha*Minimize(expr) == Maximize(-alpha*expr)

-alpha*Maximize(expr) == Minimize(-alpha*expr)

对于问题的加法和乘法规则同样简单：

# 加法和减法。

prob1 + prob2 == Problem(prob1.objective + prob2.objective,
                         prob1.constraints + prob2.constraints)

prob1 - prob2 == Problem(prob1.objective - prob2.objective,
                         prob1.constraints + prob2.constraints)

# 乘法（其中alpha是任意标量）。

alpha*prob == Problem(alpha*prob.objective, prob.constraints)

请注意，+ 运算符连接约束列表，因为这是Python列表的默认行为。 目标和问题也支持原地操作符 +=、-=, 和 *=，遵循上述相同的规则。

求解方法选项

solve 方法接受一些可选参数，可以用来改变CVXPY解析和求解问题的方式。

solve(solver=None, verbose=False, gp=False, qcp=False, requires_grad=False, enforce_dpp=False, **kwargs)

使用指定的方法解决问题。

会通过副作用将 status 和 value 属性填充到问题对象中。

Parameters:

• solver (str, 可选) – 要使用的求解器。

• verbose (bool, 可选) – 是否覆盖隐藏求解器输出的默认设置。

• gp (bool, 可选) – 如果为 True，将问题解析为遵循几何规划的问题，而不是遵循凸规划的问题。

• qcp (bool, 可选) – 如果为 True，将问题解析为遵循准凸规划的问题，而不是遵循凸规划的问题。

• requires_grad (bool, 可选) –

  通过在求解后调用 problem.backward() 方法来计算相对于 Parameters 的解的梯度， 或者通过在 Parameters 的扰动给定的情况下调用 problem.derivative() 方法来计算变量的扰动。

  仅支持 DCP 和 DGP 问题的梯度计算，不支持准凸问题。 在计算梯度时（即此参数为 True 时），问题必须满足 DPP 规则。

• enforce_dpp (bool, 可选) – 当为 True 时，尝试解决非 DPP 问题时会抛出 DPPError 异常（而不仅仅是警告）。 仅适用于涉及 Parameters 的问题。默认值为 False。

• ignore_dpp (bool, 可选) – 当为 True 时，DPP 问题会被视为非 DPP，这可能会加快编译速度。默认值为 False。

• kwargs – 用于指定求解器特定选项的其他关键字参数。

Returns:

问题的最优值，或指示无法解决问题的字符串。

我们将在下面详细讨论可选参数。

选择求解器

CVXPY可以与开源求解器 ECOS、OSQP 和 SCS 一起使用。如果单独安装其它求解器，CVXPY也可以调用它们。下表显示了支持的求解器可以处理的问题类型。

	LP	QP	SOCP	SDP	EXP	POW	MIP
CBC	X						X
CLARABEL	X	X	X	X	X	X
COPT	X	X	X	X			X*
GLOP	X
GLPK	X
GLPK_MI	X						X
OSQP	X	X
PIQP	X	X
PROXQP	X	X
PDLP	X
CPLEX	X	X	X				X
NAG	X	X	X
ECOS	X	X	X		X
GUROBI	X	X	X				X
MOSEK	X	X	X	X	X	X	X**
CVXOPT	X	X	X	X
SDPA ***	X	X	X	X
SCS	X	X	X	X	X	X
SCIP	X	X	X				X
XPRESS	X	X	X				X
SCIPY	X						X*

(*) 仅支持混合整数线性规划。

(**) 不包括混合整数半定规划。

(***) 如果安装了适当的SDPA软件包，则SDPA可以支持多精度。使用多精度支持，SDPA可以使用更小的 epsilonDash 和/或 epsilonStar 参数来解决问题。必须手动调整这些参数，以达到所需的精度。请参阅求解器网站获取详细信息。SDPA还可以使用多精度支持解决一些病态问题。

LP - 线性规划是指具有线性目标函数和线性约束的问题。

QP - 二次规划是指具有二次目标函数和线性约束的问题。

SOCP - 二阶锥规划是指具有二阶锥约束的问题。二阶锥定义为

\(\mathcal{C}_{n+1} = \left\{\begin{bmatrix} x \\ t \end{bmatrix} \mid x \in \mathbb{R}^n , t \in \mathbb{R} , \| x \|_2 \leq t\right\}\)

SDP - 半定规划是指具有 半定矩阵约束 的问题。EXP - 指的是具有指数锥约束的问题。指数锥被定义为

\(\{(x,y,z) \mid y > 0, y\exp(x/y) \leq z \} \cup \{ (x,y,z) \mid x \leq 0, y = 0, z \geq 0\}\).

POW - 指的是具有三维幂指锥约束的问题。三维幂指锥被定义为

\(\{(x,y,z) \mid x^{\alpha}y^{\alpha} \geq |z|, x \geq 0, y \geq 0 \}\).

对于幂指锥约束的支持是最近添加的（v1.1.8），CVXPY目前没有利用此约束的原子。如果您想在模型中使用这种类型的约束，您将需要手动实例化``PowCone3D``和/或``PowConeND``对象。

MIP - 混合整数规划 是指一些决策变量被限制为整数值的问题。

默认情况下，CVXPY调用最专门处理该问题类型的求解器。例如，对于SOCP问题，调用`ECOS`_。 `SCS`_可以处理所有问题（除了混合整数规划）。如果问题是QP，CVXPY将使用`OSQP`_。

您可以使用``solver``关键字参数来更改CVXPY调用的求解器。如果您选择的求解器无法解决问题，CVXPY将引发异常。以下是使用不同求解器解决相同问题的示例代码。

# 使用不同求解器解决问题。
x = cp.Variable(2)
obj = cp.Minimize(x[0] + cp.norm(x, 1))
constraints = [x >= 2]
prob = cp.Problem(obj, constraints)```python

# 用OSQP求解。
prob.solve(solver=cp.OSQP)
print("使用OSQP求解的最优值:", prob.value)

# 用ECOS求解。
prob.solve(solver=cp.ECOS)
print("使用ECOS求解的最优值:", prob.value)

# 用COPT求解。
prob.solve(solver=cp.COPT)
print("使用COPT求解的最优值:", prob.value)

# 用CVXOPT求解。
prob.solve(solver=cp.CVXOPT)
print("使用CVXOPT求解的最优值:", prob.value)

# 用SDPA求解。
prob.solve(solver=cp.SDPA)
print("使用SDPA求解的最优值:", prob.value)

# 用SCS求解。
prob.solve(solver=cp.SCS)
print("使用SCS求解的最优值:", prob.value)

# 用SciPy/HiGHS求解。
prob.solve(solver=cp.SCIPY, scipy_options={"method": "highs"})
print("使用SciPy/HiGHS求解的最优值:", prob.value)

# 用GLOP求解。
prob.solve(solver=cp.GLOP)
print("使用GLOP求解的最优值:", prob.value)

# 用GLPK求解。
prob.solve(solver=cp.GLPK)
print("使用GLPK求解的最优值:", prob.value)

# 用GLPK_MI求解。
prob.solve(solver=cp.GLPK_MI)
print("使用GLPK_MI求解的最优值:", prob.value)

# 使用 CLARABEL 求解。
prob.solve(solver=cp.CLARABEL)
print("使用 CLARABEL 的最优值：", prob.value)

# 使用 GUROBI 求解。
prob.solve(solver=cp.GUROBI)
print("使用 GUROBI 的最优值：", prob.value)

# 使用 MOSEK 求解。
prob.solve(solver=cp.MOSEK)
print("使用 MOSEK 的最优值：", prob.value)

# 使用 PIQP 求解。
prob.solve(solver=cp.PIQP)
print("使用 PIQP 的最优值：", prob.value)

# 使用 PROXQP 求解。
prob.solve(solver=cp.PROXQP)
print("使用 PROXQP 的最优值：", prob.value)

# 使用 CBC 求解。
prob.solve(solver=cp.CBC)
print("使用 CBC 的最优值：", prob.value)

# 使用 CPLEX 求解。
prob.solve(solver=cp.CPLEX)
print("使用 CPLEX 的最优值：", prob.value)

# 使用 NAG 求解。
prob.solve(solver=cp.NAG)
print("使用 NAG 的最优值：", prob.value)

# 使用 PDLP 求解。
prob.solve(solver=cp.PDLP)
print("使用 PDLP 的最优值：", prob.value)

# 使用 SCIP 求解。
prob.solve(solver=cp.SCIP)
print("使用 SCIP 的最优值：", prob.value)

# 使用XPRESS求解。
prob.solve(solver=cp.XPRESS)
print("使用XPRESS求解的最优值：", prob.value)

使用OSQP求解的最优值：6.0
...
使用XPRESS求解的最优值：6.0

使用 installed_solvers 实用函数获取您安装的CVXPY支持的求解器列表。

print(installed_solvers())

['CBC', 'CVXOPT', 'MOSEK', 'GLPK', 'GLPK_MI', 'ECOS', 'SCS', 'SDPA'
 'SCIPY', 'GUROBI', 'OSQP', 'CPLEX', 'NAG', 'SCIP', 'XPRESS', 'PROXQP']

查看求解器输出

所有求解器都可以打印出关于它们在求解问题时的进展的信息。这些信息在调试求解器错误时很有用。要查看求解器的输出，请在求解方法中设置 verbose=True。

# 用ECOS解决问题并显示输出。
prob.solve(solver=cp.ECOS, verbose=True)
print(f"使用ECOS的最优值：{prob.value}")

ECOS 1.0.3 - (c) A. Domahidi, Automatic Control Laboratory, ETH Zurich, 2012-2014.

It     pcost         dcost      gap     pres    dres     k/t     mu      step     IR
 0   +0.000e+00   +4.000e+00   +2e+01   2e+00   1e+00   1e+00   3e+00    N/A     1 1 -
 1   +6.451e+00   +8.125e+00   +5e+00   7e-01   5e-01   7e-01   7e-01   0.7857   1 1 1
 2   +6.788e+00   +6.839e+00   +9e-02   1e-02   8e-03   3e-02   2e-02   0.9829   1 1 1
 3   +6.828e+00   +6.829e+00   +1e-03   1e-04   8e-05   3e-04   2e-04   0.9899   1 1 1
 4   +6.828e+00   +6.828e+00   +1e-05   1e-06   8e-07   3e-06   2e-06   0.9899   2 1 1
 5   +6.828e+00   +6.828e+00   +1e-07   1e-08   8e-09   4e-08   2e-08   0.9899   2 1 1

最优解（在feastol=1.3e-08、reltol=1.5e-08、abstol=1.0e-07的条件下）。
运行时间：0.000121秒。

使用ECOS的最优值：6.82842708233

求解有纪律的几何规划

当使用 gp=True 调用 solve 方法时，问题被解析为有纪律的几何规划，而不是有纪律的凸规划。 更多信息，请参见 DGP 教程 。

求解器统计信息

当在问题对象上调用 solve 方法并调用求解器时，问题对象会记录最优值、原始和对偶变量的值以及几个求解器统计信息。 我们已经讨论了如何查看最优值和变量值。 求解器统计信息可以通过 problem.solver_stats 属性访问，该属性返回一个 SolverStats 对象。 例如， problem.solver_stats.solve_time 给出求解器求解问题所需的时间。

Note

存储在 problem.solver_stats 中的信息因所使用的求解器而异。 例如，如果我们使用 MOSEK ， problem.solver_stats.num_iters 包括以下内容： iinfitem.intpnt_iter、liinfitem.simplex_iter 或``iinfitem.mio_num_relax``。此外， problem.solver_stats.extra_stats 包括 liinfitem.mio_intpnt_iter 和 liinfitem.mio_simplex_iter。 有关更多信息，请访问 https://docs.mosek.com/latest/pythonapi/constants.html

热启动

当对一个参数的多个值求解相同的问题时，许多求解器可以利用以前求解的工作（即，热启动）。 例如，求解器可以使用先前的解作为初始点或重用缓存的矩阵分解。 热启动默认情况下是启用的，并由 warm_start 求解器选项控制。 下面的代码展示了如何通过热启动加速求解一系列相关的最小二乘问题。

import cvxpy as cp
import numpy

# 问题数据。
m = 2000
n = 1000
numpy.random.seed(1)
A = numpy.random.randn(m, n)
b = cp.Parameter(m)

# 构造问题。
x = cp.Variable(n)
prob = cp.Problem(cp.Minimize(cp.sum_squares(A @ x - b)),
                   [x >= 0])

b.value = numpy.random.randn(m)
prob.solve()
print("第一个求解时间:", prob.solver_stats.solve_time)

b.value = numpy.random.randn(m)
prob.solve(warm_start=True)
print("Second solve time:", prob.solver_stats.solve_time)

第一个求解时间：11.14
第二次求解时间：2.95

在这种情况下，速度的提升来自于缓存KKT矩阵的因式分解。 如果``A``是一个参数，那么因式分解的缓存将不可能，热启动的好处只是一个良好的初始点。

热启动也可以在第一次求解问题时提供一个初始猜测。 初始猜测是根据问题变量的``value``字段构造的。 如果同一个问题被解决了第二次，初始猜测将根据上述缓存的先前解决方案构造 （而不是根据``value``字段）。

设置求解器选项

OSQP、ECOS、GLOP、MOSEK、CBC、CVXOPT、NAG、PDLP、GUROBI、SCS 、CLARABEL、PIQP 和 PROXQP 的Python接口允许您设置求解器选项，如最大迭代次数。您可以通过CVXPY将这些选项作为关键字参数传递。

例如，在这里我们告诉SCS使用间接方法解决线性方程，而不是直接方法。

# 使用SCS进行求解，使用稀疏间接方法。
prob.solve(solver=cp.SCS, verbose=True, use_indirect=True)
print(f"SCS求解的最优值：{prob.value}")

----------------------------------------------------------------------------
    SCS v1.0.5 - Splitting Conic Solver
    (c) Brendan O'Donoghue, Stanford University, 2012
----------------------------------------------------------------------------
Lin-sys: sparse-indirect, nnz in A = 13, CG tol ~ 1/iter^(2.00)
EPS = 1.00e-03, ALPHA = 1.80, MAX_ITERS = 2500, NORMALIZE = 1, SCALE = 5.00
Variables n = 5, constraints m = 9
Cones:  linear vars: 6
    soc vars: 3, soc blks: 1
Setup time: 2.78e-04s
----------------------------------------------------------------------------
 Iter | pri res | dua res | rel gap | pri obj | dua obj | kap/tau | time (s)
----------------------------------------------------------------------------
     0| 4.60e+00  5.78e-01       nan      -inf       inf       inf  3.86e-05
    60| 3.92e-05  1.12e-04  6.64e-06  6.83e+00  6.83e+00  1.41e-17  9.51e-05
----------------------------------------------------------------------------
Status: Solved
Timing: Total solve time: 9.76e-05s
    Lin-sys: avg # CG iterations: 1.00, avg solve time: 2.24e-07s
    Cones: avg projection time: 4.90e-08s
----------------------------------------------------------------------------
Error metrics:
|Ax + s - b|_2 / (1 + |b|_2) = 3.9223e-05
|A'y + c|_2 / (1 + |c|_2) = 1.1168e-04
|c'x + b'y| / (1 + |c'x| + |b'y|) = 6.6446e-06
dist(s, K) = 0, dist(y, K*) = 0, s'y = 0
----------------------------------------------------------------------------
c'x = 6.8284, -b'y = 6.8285
============================================================================
optimal value with SCS: 6.82837896975

这是求解器选项的完整列表。

`OSQP`_选项：

'max_iter'

最大迭代次数（默认：10,000）。

'eps_abs'

绝对精度（默认：1e-5）。

'eps_rel'

相对精度（默认：1e-5）。

其他选项请参见 `OSQP文档<https://osqp.org/docs/interfaces/solver_settings.html>`_ 。

PROXQP`_选项：`’backend’``

求解器后端 [dense, sparse] (默认: dense).

'max_iter'

最大迭代次数 (默认: 10,000).

'eps_abs'

绝对精度 (默认: 1e-8).

'eps_rel'

相对精度 (默认: 0.0).

'rho'

主要近端参数 (默认: 1e-6).

'mu_eq'

对偶等式约束近端参数 (默认: 1e-3).

'mu_in'

对偶不等式约束近端参数 (默认: 1e-1).

`ECOS`_选项:

'max_iters'

最大迭代次数 (默认: 100).

'abstol'

绝对精度 (默认: 1e-8).

'reltol'

相对精度（默认值：1e-8）。

'feastol'

可行性条件的容差（默认值：1e-8）。

'abstol_inacc'

用于不准确解的绝对精度（默认值：5e-5）。

'reltol_inacc'

用于不准确解的相对精度（默认值：5e-5）。

'feastol_inacc'

用于不准确解的可行性条件容差（默认值：1e-4）。

GLOP 选项：

'time_limit_sec'

解法的时间限制，以秒为单位。

'parameters_proto'

A ortools.glop.parameters_pb2.GlopParameters protocol buffer message. GlopParameters 的定义，请参见 此处。

MOSEK 选项：

'mosek_params'

一个以 name: value 形式的 MOSEK 参数字典。参数名称应为字符串，与 MOSEK C API 或命令行中的名称相同，例如 'MSK_DPAR_BASIS_TOL_X'， 'MSK_IPAR_NUM_THREADS' 等。值可以是字符串、整数或浮点数，具体取决于参数。 请参考 示例。'save_file' 一个文件的名称，MOSEK将在优化之前保存问题。 请参考MOSEK文档获取支持的文件格式列表。文件格式是根据扩展名选择的。

'bfs'

对于线性问题，如果 bfs=True ，则将检索基本解而不是内点解。 这假设没有使用阻止计算基本解的特定MOSEK参数。

'accept_unknown'

如果 accept_unknown=True ，即使求解器在给定条件下没有生成最优点，也会返回一个不准确的解决方案， 即使它任意糟糕。

'eps'

对于（锥形）内点、单纯形和MIO求解器，对终止参数应用公差 eps 。 终止参数的完整列表可以通过 MOSEK.tolerance_params() 在 cvxpy.reductions.solvers.conic_solvers.mosek_conif 中返回。 显式定义的参数优先于 eps 。

Note

在CVXPY 1.1.6中，我们对MOSEK接口进行了完全重写。主要变化是我们现在对所有连续问题进行对偶化。 对偶化是自动完成的，因为它消除了以前对大量松弛变量的需求，并且与我们旧的MOSEK接口相比，永不导致更大的问题。 如果你注意到在CVXPY 1.1.6或更高版本下，某些问题的MOSEK求解时间较慢，请务必使用MOSEK求解器选项告诉MOSEK它应该求解对偶问题； 这可以通过将键值对 ('MSK_IPAR_INTPNT_SOLVE_FORM', 'MSK_SOLVE_DUAL') 添加到 mosek_params 参数中来实现。

CVXOPT 选项：

'max_iters'

最大迭代次数（默认值：100）。

'abstol'

绝对精度（默认值：1e-7）。

'reltol'

相对精度（默认值：1e-6）。

'feastol'

可行性条件的公差（默认值：1e-7）。 'refinement' 在求解KKT系统后的迭代细化步骤的数量（默认为1）。

'kktsolver'

控制CVXOPT内点算法在每个步骤中用于求解线性方程组的方法。此参数可以是一个字符串（具有几个值之一）或一个函数句柄。

CVXOPT内建的KKT求解器可以用字符串 ‘ldl’、’ldl2’、’qr’、’chol’ 和 ‘chol2’ 来指定。如果选择 ‘chol’，CVXPY将执行额外的前处理过程来消除多余的约束条件。还可以设置 kktsolver='robust'。’robust’求解器是用Python实现的，是CVXPY源代码的一部分；’robust’求解器不需要前处理阶段来消除多余的约束条件，但可能比 ‘chol’ 求解器慢。

最后，还有一个选项可以传递一个函数句柄作为 kktsolver 参数。使用基于函数句柄的KKT求解器可以完全控制CVXOPT内点算法中遇到的线性系统的求解。这种形式的KKT求解器的API是对CVXOPT的函数句柄KKT求解器的API的一个小包装。CVXPY用户所遵循的精确API在CVXPY源代码中描述： cvxpy/reductions/solvers/kktsolver.py。

`SDPA`_选项：

'maxIteration'

最大迭代次数。（默认为100）。

'epsilonStar'

对于主优化问题和对偶优化问题的近似最优解的精度。（默认为1.0E-7）。

'lambdaStar'

初始点。（默认为1.0E2）。

'omegaStar'

用于搜索最优解的搜索区域。（默认为2.0）。

'lowerBound'

主优化问题最小目标值的下界。（默认为-1.0E5）。

'upperBound'

对偶优化问题最大目标值的上界。（默认为1.0E5）。'betaStar' 当当前点可行时，控制搜索方向的参数。（默认值：0.1）。

'betaBar'

当当前点不可行时，控制搜索方向的参数。（默认值：0.2）。

'gammaStar'

主要和对偶步长的缩小因子。（默认值：0.9）。

'epsilonDash'

在原始和对偶SDP之间的近似最优解的相对精确度。（默认值：1.0E-7）。

'isSymmetric'

指定是否检查输入矩阵的对称性。（默认值：False）。

'isDimacs'

指定是否计算DIMACS误差。（默认值：False）。

'numThreads'

numThreads（默认值：'multiprocessing.cpu_count()'）。

'domainMethod'

利用定义域中的稀疏性的算法选项。可以是``’none’（不利用定义域中的稀疏性）或’basis’（使用基准表示）（默认值：’none’``）。

'rangeMethod'

利用值域中的稀疏性的算法选项。可以是``’none’（不利用值域中的稀疏性）或’decomp’（使用矩阵分解）（默认值：’none’``）。

'frvMethod'

消除自由变量的方法。可以是``’split’或’elimination’（默认值：’split’）。’rho’``

参数标识split方法的范围或消元方法的枢轴。 （默认值：0.0）。

'zeroPoint'

矩阵操作的零点，决定不可解性或LU分解。 （默认值：1.0E-12）。

`SCS`_选项：

'max_iters'

最大迭代次数（默认值：2500）。

'eps'

收敛容差（默认值：1e-4）。

'alpha'

松弛参数（默认值：1.8）。

'acceleration_lookback'

SCS 2.0及更高版本的Anderson加速参数。它可以是任何正数或负数整数；默认值为10。有关更多信息，请参见 SCS文档的此页面 。

Warning

该参数的值往往影响SCS 2.X是否能收敛到准确解。如果*未显式*设置``acceleration_lookback``且SCS 2.X无法收敛， 则CVXPY将发出警告并尝试使用``acceleration_lookback=0``重新求解问题。如果您使用的是SCS 3.0或更高版本，则不会尝试重新求解问题。

'scale'

在最小化原始和对偶残差之间的平衡（默认值：5.0）。

'normalize'

是否对数据矩阵进行预处理（默认值：True）。'use_indirect' 是否使用间接求解器来解决KKT系统（而不是直接求解器）（默认值：True）。

'use_quad_obj'

是否使用二次目标函数或将其约束为SOC约束（默认值：True）。

`CBC`_选项：

通过`CGL`_进行割集生成

一般说明：

• 其中一些割集生成器似乎存在错误（使用AllDifferentCuts，RedSplitCuts，LandPCuts，PreProcessCuts时发现问题）

• 即使 'verbose=False'，其中一些割集生成器也会产生嘈杂的输出

可用的割集生成器有：

GomoryCuts，MIRCuts，MIRCuts2，TwoMIRCuts，ResidualCapacityCuts，KnapsackCuts，FlowCoverCuts，CliqueCuts，LiftProjectCuts，AllDifferentCuts，OddHoleCuts，RedSplitCuts，LandPCuts，PreProcessCuts，ProbingCuts，SimpleRoundingCuts。

'CutGenName'

如果割集生成器被激活（例如 'GomoryCuts=True'）

'integerTolerance'

如果整数变量与整数值之间的差值不超过此值（容差），则认为它在整数值附近

'maximumSeconds'

在给定的秒数后停止求解

'maximumNodes'

在给定的最大节点数后停止求解``’maximumSolutions’`` 在评估x个解之后停止

'numberThreads'

设置线程数

'allowableGap'

如果最优解与最佳可能解之间的差距小于此值，则返回一个解。

'allowableFractionGap'

如果最优解与最佳可能解之间的差距小于此分数，则返回一个解。

'allowablePercentageGap'

如果最优解与最佳可能解之间的差距小于此百分比，则返回一个解。

COPT 选项：

COPT求解器选项在CVXPY中作为关键字参数指定。完整的COPT参数列表（包括默认值）在 此处 列出。

CPLEX 选项：

'cplex_params'

一个字典，其中键值对由参数名（与CPLEX Python API中使用的名称相同）和参数值组成。例如，要设置高级启动开关参数（即CPX_PARAM_ADVIND），使用参数名”advance”。要使用数据一致性检查和建模辅助参数（即CPX_PARAM_DATACHECK），使用参数名”read.datacheck”，依此类推。

'cplex_filename'

一个字符串，指定问题将被写入的文件名。例如，使用”model.lp”、”model.sav”或”model.mps”分别导出到LP、SAV和MPS格式。reoptimize 一个布尔值。这只适用于CPLEX初步产生“无可行解或无界解”状态的问题。它的默认值为False。如果设置为True，那么如果CPLEX产生“无可行解或无界解”状态，则会自动更改其算法参数，并重新求解问题以确定其精确状态。

reoptimize

一个布尔型变量。仅适用于 CPLEX 最初产生 “不可行或无约束 “状态的问题。 默认值为 “假”。如果设置为 “真”，那么如果 CPLEX 产生 “不可行或无约束 “状态，其算法 参数会自动更改，并重新求解问题以确定其精确状态。

NAG 选项:

'nag_params'

一个包含NAG选项参数的字典。有关详细信息，请参阅NAG的Python或Fortran API。例如，要将线性规划问题的最大迭代次数设置为20，可以使用”LPIPM Iteration Limit”作为键名称，并将其值设置为20。

SCIP 选项： 'scip_params' 一个包含SCIP可选参数的字典，`这里 <https://www.scipopt.org/doc-5.0.1/html/PARAMETERS.php>`_列出了所有参数及其默认值。

SCIPY 选项： 'scipy_options' 一个包含SciPy可选参数的字典，`这里 <https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html#scipy.optimize.linprog>`_列出了所有参数及其默认值。

• 请注意：所有选项都应在``’scipy_options’字典内以键值对的形式列出，不应该使用嵌套的选项字典。某些方法具有不同的参数，请检查您希望使用的方法的参数，例如，对于method = 'highs-ipm'。另外，请注意，'integrality'和'bounds'选项不应在’scipy_options’``内指定，而应使用CVXPY来指定。

• 此求解器的主要优势是其能够使用用C++编码的`HiGHS`_ LP和MIP求解器。但是，这些求解器要求SciPy的版本大于1.6.1和1.9.0。要使用`HiGHS`_ LP求解器，只需将method参数设置为’highs-ds’（双入口法），’highs-ipm’（内点法）或’highs’（将自动选择’highs-ds’或’highs-ipm’）。要使用`HiGHS`_ MIP求解器，不设置method参数或将其明确设置为’highs’。

PDLP 选项：

'time_limit_sec'

解决的时间限制，以秒为单位。

'parameters_proto'

一个 ortools.pdlp.solvers_pb2.PrimalDualHybridGradientParams 协议缓冲区消息。有关PrimalDualHybridGradientParams的定义，请参阅 这里 。GUROBI 选项：

Gurobi求解器选项在CVXPY中被指定为关键字参数。包含默认值的Gurobi参数的完整列表在此处列出 here.

除了Gurobi的参数之外，还有以下选项可用：

'env'

允许传递一个Gurobi环境，该环境指定了参数和许可证信息。关键字参数将覆盖此环境中的任何设置。

reoptimize

一个布尔值。这仅在GUROBI最初产生“infeasible or unbounded”状态的问题中才相关。它的默认值为False。如果设置为True， 那么如果GUROBI产生了“infeasible or unbounded”状态，它的算法参数会自动改变，并重新求解问题以确定其详细状态。

`CLARABEL`_选项：

'max_iter'

最大迭代次数（默认值：50）。

'time_limit'

时间限制（默认值：0.0，表示无限制）。

其他选项请参阅 CLARABEL文档.

`XPRESS`_选项：

'save_iis'

是否在发现问题为不可行时保存不可约化的不可行子系统（IIS）。如果为0（默认值），则不保存IIS；如果为负数，则保存所有的IIS；如果为正数``’k>0’，则最多保存’k’``个IIS。

'write_mps'

Xpress将保存二次或圆锥问题的文件名（扩展名为``’.mps’``）。

'maxtime'

时间限制（以秒为单位，必须为整数）。

你可以在 'solve' 命令中指定Xpress Optimizer的所有控制选项。有关所有控制选项，请参阅 `FICO Xpress Optimizer手册<https://www.fico.com/fico-xpress-optimization/docs/dms2019-03/solver/optimizer/HTML/chapter7.html>`_ 。

`PIQP`_选项：

'backend'

求解器后端[dense, sparse]（默认值：sparse）。

'max_iter'

最大迭代次数（默认值：250）。

'eps_abs'

绝对精度（默认值：1e-8）。

'eps_rel'

相对精度（默认值：1e-9）。

其他选项请参阅 PIQP文档 。

获取标准形式

如果您对获取CVXPY为问题生成的标准形式感兴趣，可以使用 get_problem_data 方法。当问题被解决时， SolvingChain 通过一个与目标求解器兼容的底层表示将问题 传递给求解器，求解问题。该方法返回该底层表示以及用于将解包的 SolvingChain 和元数据 到问题中。该底层表示与传递给求解器的参数非常相似，但并不相同。

可以通过调用返回的求解链上的 solve_via_data 方法，使用数据来获得等价的底层问题的解， 该方法是一个包装器，可以进一步处理和求解问题的CVXPY外部代码来实现。通过调用 unpack_results 方法 来恢复原始问题的解。

例如：

problem = cp.Problem(objective, constraints)
data, chain, inverse_data = problem.get_problem_data(cp.SCS)
# 使用 `data` 调用SCS
soln = chain.solve_via_data(problem, data)
# 将SCS返回的解解包到 `problem` 中
problem.unpack_results(soln, chain, inverse_data)

或者，此方法返回的 data 字典包含足够的信息来绕过CVXPY并直接调用求解器。

例如：

problem = cp.Problem(objective, constraints)
probdata, _, _ = problem.get_problem_data(cp.SCS)

import scs
data = {
  'A': probdata['A'],
  'b': probdata['b'],
  'c': probdata['c'],
}
cone_dims = probdata['dims']
cones = {
    "f": cone_dims.zero,
    "l": cone_dims.nonpos,
    "q": cone_dims.soc,
    "ep": cone_dims.exp,
    "s": cone_dims.psd,
}
soln = scs.solve(data, cones)

CVXPY返回的data字典的结构取决于求解器。要获取详细信息，请打印字典，或查阅 cvxpy/reductions/solvers 中的求解器接口。

规约

CVXPY使用一种称为 reductions 的系统，将用户提供的问题从其形式重写为求解器会接受的标准形式。规约是从一个问题到另一个等价问题的转换。如果一个问题的解可以有效地转换为另一个问题的解，则这两个问题是等价的。 规约把CVXPY问题作为输入，并输出一个CVXPY问题。详细讨论可用的规约集合在 简化

纪律化参数化编程

注意：DPP要求CVXPY的版本为1.1.0或更高版本。

Parameters 是常数的符号表示。使用参数可以修改常数的值，而无需重构整个问题。当您的参数化问题根据*纪律化参数化编程（DPP）*构建时，针对不同参数值重复求解问题可以比重复求解新问题更快。

如果您打算多次求解一个 凸约束规划问题 (DCP) 或 凹约束规划问题 (DGP)，并且针对数值数据的不同值进行求解，或者如果您想通过DCP或DGP问题的解映射进行微分的话，您应该阅读本教程。

什么是DPP？

DPP是一套用于生成符合纪律化参数化凸约束规划（DCP）或凹约束规划（DGP）的参数化问题的规则集。CVXPY可以非常快速地重新规范化DPP符合的问题。当求解DPP问题的第一次时，CVXPY会编译它并缓存参数与问题数据之间的映射。因此，对DPP问题的后续重写可以大大加快速度。CVXPY允许您解决不符合DPP的参数化问题，但在这样做时不会看到加速效果。

DPP规则集

DPP对DCP和DGP问题中的表达式如何输入参数施加了一些限制。首先，我们介绍DCP问题的DPP规则集。然后，我们介绍DGP问题的DPP规则集。

DCP问题。 在DPP中，如果一个表达式不涉及变量并且在其参数中是仿射的，则称其为参数仿射表达式；如果一个表达式没有参数，则称其为无参数表达式。DPP对DCP引入了两个限制条件：

1. 根据DPP的规定，所有参数都被归类为仿射，就像变量一样。

2. 根据DPP的规定，当至少一个表达式为常量时，或一个表达式为参数仿射表达式且另一个表达式为无参数表达式时，两个表达式的乘积是仿射的。

如果一个表达式符合DPP，则表示它在这两个限制条件下符合DCP。您可以通过使用关键字参数``is_dcp``并将其设为``dpp=True``（默认情况下，此关键字参数为``False``）来检查一个表达式或问题是否符合DPP。例如，

import cvxpy as cp


m, n = 3, 2
x = cp.Variable((n, 1))
F = cp.Parameter((m, n))
G = cp.Parameter((m, n))
g = cp.Parameter((m, 1))
gamma = cp.Parameter(nonneg=True)

objective = cp.norm((F + G) @ x - g) + gamma * cp.norm(x)
print(objective.is_dcp(dpp=True))

输出``True``。我们可以按照DPP的分析来理解为什么``objective``是符合DPP的。乘积``(F + G) @ x``在DPP下是仿射的，因为``F + G``是参数仿射表达式，而``x``是无参数表达式。差值``(F + G) @ x - g``在DPP下是仿射的，因为加法原子是仿射的，并且``(F + G) @ x``和``- g``都是仿射的。同样，``gamma * cp.norm(x)``在DPP下是仿射的，因为``gamma``是参数仿射表达式，``cp.norm(x)``是无参数表达式。最终的目标函数在DPP下是仿射的，因为加法是仿射的。

有些表达式是DCP符合但不符合DPP的。例如，DPP禁止对两个带参数的表达式进行乘积运算：

import cvxpy as cp


x = cp.Variable()
gamma = cp.Parameter(nonneg=True)
problem = cp.Problem(cp.Minimize(gamma * gamma * x), [x >= 1])
print("是否为 DPP？", problem.is_dcp(dpp=True))
print("是否为 DCP？", problem.is_dcp(dpp=False))

此代码片段输出结果为

是否为 DPP？ False
是否为 DCP？ True

就像可以通过符合 DCP 规范的方式重写非 DCP 问题一样， 也可以通过符合 DPP 规范的方式重新表达非 DPP 问题。 例如，上述问题可以等价地重写为

import cvxpy as cp


x = cp.Variable()
y = cp.Variable()
gamma = cp.Parameter(nonneg=True)
problem = cp.Problem(cp.Minimize(gamma * y), [y == gamma * x])
print("是否为 DPP？", problem.is_dcp(dpp=True))
print("是否为 DCP？", problem.is_dcp(dpp=False))这段代码打印：

是 DPP 吗？True
是 DCP 吗？True

在其他情况下，你可以通过在 DSL 之外进行非 DPP 转换来表示参数的非 DPP 变换， 例如在 NumPy 中。例如，如果 P 是一个参数，x 是一个变量， cp.quad_form(x, P) 就不是 DPP。你可以这样表示一个参数化二次形式：

import cvxpy as cp
import numpy as np
import scipy.linalg


n = 4
L = np.random.randn(n, n)
P = L.T @ L
P_sqrt = cp.Parameter((n, n))
x = cp.Variable((n, 1))
quad_form = cp.sum_squares(P_sqrt @ x)
P_sqrt.value = scipy.linalg.sqrtm(P)
assert quad_form.is_dcp(dpp=True)

作为另一个例子，当 p 是一个参数时，商 expr / p 不符合 DPP 标准， 但可以将其重写为 expr * p_tilde，其中 p_tilde 是一个表示 1/p 的参数。

DGP 问题。 就像 DCP 是 DGP 的 log-log 类比一样，DPP 是 DGP 的 log-log 类比的 DPP。DPP 对 DGP 引入了两个限制：

1. 在 DPP 下，所有的正参数都被分类为 log-log-affine，就像正变量一样。

2. 在 DPP 下，幂项 x**p``（以 ``x 为底，以 p 为指数） 只要 x 和 p 都不是参数化的，它就是 log-log 仿射的。请注意，对于幂次，指数 p 必须是一个数值常数或者一个参数；如果试图构造一个指数为复合表达式的幂原子，例如 x**(p + p)，其中 p 是一个参数，会导致 ValueError。

在 DGP 问题中，如果一个参数作为指数出现，它可以有任何符号。如果一个参数在 DGP 问题的其他地方出现，它必须是正的，即它必须使用 cp.Parameter(pos=True) 构造。

您可以通过使用关键字参数 dpp=True 来调用 is_dgp 方法来检查一个表达式或问题是否符合 DPP 规定（默认情况下，这个关键字参数为 False）。例如，

import cvxpy as cp


x = cp.Variable(pos=True)
y = cp.Variable(pos=True)
a = cp.Parameter()
b = cp.Parameter()
c = cp.Parameter(pos=True)

monomial = c * x**a * y**b
print(monomial.is_dgp(dpp=True))

打印出 True。表达式 x**a 和 y**b 是对数-对数仿射的，因为它们不包含参数。参数 c 是对数-对数仿射的，因为它是正数，而且单项式表达式是对数-对数仿射的，因为对数-对数仿射表达式的乘积也是对数-对数仿射的。

有些表达式是符合 DGP 规范但不符合 DPP 规范的。例如，DPP 禁止将一个参数化的表达式提升为一个幂次：

import cvxpy as cp


x = cp.Variable(pos=True)
a = cp.Parameter()

monomial = (x**a)**a
print("Is DPP? ", monomial.is_dgp(dpp=True))
print("Is DGP? ", monomial.is_dgp(dpp=False))

这段代码输出：

Is DPP? False
Is DGP? True

可以通过在 CVXPY 之外进行参数的非 DPP 变换来表示参数的非 DPP 变换，例如使用 NumPy。例如，可以将上述程序重写为以下符合 DPP 的程序：

import cvxpy as cp


a = 2.0
x = cp.Variable(pos=True)
b = cp.Parameter(value=a**2)

monomial = x**b

反复求解 DPP 问题

下面的例子演示了如何通过使用参数来加速反复求解一个符合 DPP 要求的 DCP 问题。

import cvxpy as cp
import numpy
import matplotlib.pyplot as plt
import time

n = 15
m = 10
numpy.random.seed(1)
A = numpy.random.randn(n, m)
b = numpy.random.randn(n)
# gamma must be nonnegative due to DCP rules.
gamma = cp.Parameter(nonneg=True)

x = cp.Variable(m)
error = cp.sum_squares(A @ x - b)
obj = cp.Minimize(error + gamma*cp.norm(x, 1))
problem = cp.Problem(obj)
assert problem.is_dcp(dpp=True)

gamma_vals = numpy.logspace(-4, 1)
times = []
new_problem_times = []
for val in gamma_vals:
    gamma.value = val
    start = time.time()
    problem.solve()
    end = time.time()
    times.append(end - start)
    new_problem = cp.Problem(obj)
    start = time.time()
    new_problem.solve()
    end = time.time()
    new_problem_times.append(end - start)

plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.figure(figsize=(6, 6))
plt.plot(gamma_vals, times, label='Re-solving a DPP problem')
plt.plot(gamma_vals, new_problem_times, label='Solving a new problem')
plt.xlabel(r'$\gamma$', fontsize=16)
plt.ylabel(r'time (s)', fontsize=16)
plt.legend()

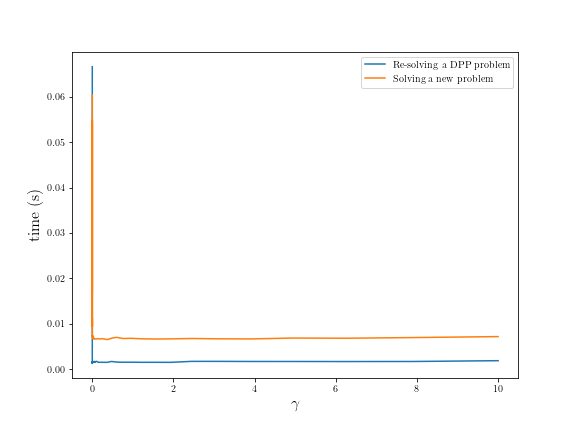
类似的加速可以用于 DGP 问题。

灵敏度分析和梯度

注意：此特性需要 CVXPY 版本 1.1.0 或更高版本支持。

一个优化问题可以被视为一个将参数映射到解的函数。这个解映射有时是可微的。CVXPY 内置了对问题的最优变量值相对于参数的微小扰动（即问题中的 “Parameter” 实例）的导数的支持。问题类公开了与计算导数相关的两个方法。 derivative 评估给定参数扰动的导数。 这使您可以计算在参数发生小变化时问题的解将如何变化，而无需重新解决问题。 backward 方法评估导数的伴随方法，计算解相对于参数的梯度。 在与自动微分软件结合使用时，这可能非常有用。

只有在问题包含参数时，导数和backward方法才有意义。 为了使问题可微分，它必须是 DPP兼容 的。 CVXPY可以计算任何DPP兼容的DCP或DGP问题的导数。在不可微分点，CVXPY计算启发式量。

例子。

作为第一个例子，我们解决一个具有解析解的简单问题， 以说明 backward 和 derivative 函数的用法。在下面的代码块中，我们构造了一个问题， 其中包含一个标量变量 x 和一个标量参数 p 。问题是最小化二次方程 (x-2*p)**2 。

import cvxpy as cp

x = cp.Variable()
p = cp.Parameter()
quadratic = cp.square(x - 2 * p)
problem = cp.Problem(cp.Minimize(quadratic))

接下来，我们为特定值``p == 3``解决问题。注意当解决问题时，我们向``solve``方法提供了关键字参数``requires_grad=True``。

p.value = 3.
problem.solve(requires_grad=True)

解决了 requires_grad=True 的问题之后，我们现在可以使用 backward 和 derivative 来对问题进行微分。首先，通过调用 backward() 方法，我们计算出解对其参数的梯度。作为副作用，backward() 方法会在所有参数上填充 gradient 属性，该属性表示解对该参数的梯度。

problem.backward()
print("梯度为 {0:0.1f}。".format(p.gradient))

在这种情况下，问题有一个平凡的解析解 2*p，因此梯度就是2。因此，正如我们所预期的，上面的代码会打印出

梯度为 2.0。

接下来，我们使用 derivative 方法来看看在 p 发生微小变化时，解 x 会如何变化。我们将通过 1e-5 来扰动 p，即 p.delta = 1e-5，调用 derivative 方法将使用一阶近似（即 dx/dp * p.delta）填充 x 的 delta 属性，表示 x 的变化。

p.delta = 1e-5
problem.derivative()
print("x.delta 为 {0:2.1g}。".format(x.delta))

在这种情况下，解是平凡的，其导数也是 2*p，因此我们知道 x 的变化应该为 2e-5。正如我们所预期的，输出结果为

x.delta 是 2e-05。

我们强调这个例子是微不足道的，因为它有一个微不足道的解析解和微不足道的导数。backward() 和 forward() 方法很有用，因为大多数凸优化问题没有解析解：在这些情况下，CVXPY可以计算解和它们的导数，尽管无法手动推导出它们。

注意。 在这个简单的例子中，变量 x 是一个标量，所以 backward 方法计算了 x 对 p 的梯度。当存在多个标量变量时，默认情况下，backward 计算了最优变量值的*和*对参数的梯度。

更一般地，backward 方法可以用来计算最优变量的标量函数 f 对参数的梯度。如果 x(p) 表示参数 p 的特定值的变量（可能是向量或矩阵）的最优值，并且 f(x(p)) 是一个标量，则 backward 可以用来计算 f 对 p 的梯度。设 x* = x(p)，假设 f 对 x* 的导数是 dx。在调用 problem.backward() 之前，只需要设置 x.gradient = dx，就可以计算出 f 对 p 的导数。

当与自动微分软件结合使用时，backward 方法非常强大。我们推荐使用软件包 CVXPY Layers，它为CVXPY问题提供了可微分的PyTorch和TensorFlow封装。

backward 还是 derivative？ 当您需要解的梯度（一个标量值函数）相对于参数的梯度时，应使用 backward 方法。如果您只想进行敏感性分析，也就是说，如果您只关心解在某些参数发生变化时会如何变化，那么应该使用 derivative 方法。当存在多个变量时，使用导数方法计算敏感度比多次调用 backward 计算整个雅可比矩阵更高效（可以通过调用多次，每次使用标准基向量）。

下一步。 请参阅关于导数的 介绍性notebook。

自定义求解器

虽然 cvxpy 默认支持许多不同的求解器，但也可以定义和使用自定义求解器。这在原型设计或开发针对特定应用程序的定制求解器时非常有用。要实现这个功能，您需要创建一个求解器类，它是 cvxpy.reductions.solvers.qp_solvers.qp_solver.QpSolver 或者 cvxpy.reductions.solvers.conic_solvers.conic_solver.ConicSolver 的子类。然后，将该求解器类的一个实例作为参数传递给 solver.solve(.)，如下所示：

import cvxpy as cp
from cvxpy.reductions.solvers.qp_solvers.osqp_qpif import OSQP


class CUSTOM_OSQP(OSQP):
    MIP_CAPABLE=False

    def name(self):
        return "CUSTOM_OSQP"

    def solve_via_data(self, *args, **kwargs):
        print("正在使用自定义 QP 求解器求解！")
        super().solve_via_data(*args, **kwargs)


x = cp.Variable()
quadratic = cp.square(x)
problem = cp.Problem(cp.Minimize(quadratic))
problem.solve(solver=CUSTOM_OSQP())

您可能还想要覆盖 Solver 类的 invert 和 import_solver 方法。

请注意，name 属性返回的字符串应与所有官方支持的求解器名称不同（可以在 cvxpy.settings.SOLVERS 中找到它们的列表）。此外，如果您的求解器支持混合整数问题，您需要将类变量 MIP_CAPABLE 设置为 True。如果您的求解器既支持混合整数问题，又是一个锥形求解器（而不是 QP 求解器），您需要将类变量 MI_SUPPORTED_CONSTRAINTS 设置为在解决混合整数问题时支持的锥形列表。通常情况下，MI_SUPPORTED_CONSTRAINTS 将与类变量 SUPPORTED_CONSTRAINTS 相同。

规范化后端

用户可以通过将 canon_backend 关键参数添加到 .solve() 方法的调用中来选择多个规范化后端，例如 problem.solve(canon_backend=cp.SCIPY_CANON_BACKEND) (CVXPY 1.3 引入)。这可以显著加快某些问题的规范化时间。 当前支持以下规范化后端:

• CPP (默认): 原始的 C++ 实现，也称为 CVXCORE。

• SCIPY: 基于 SciPy 稀疏模块的纯 Python 实现。

  对于已经向量化的问题通常很快。

• NUMPY: 纯 NumPy 的参考实现。对于一些小型或稠密问题很快。