标准凸规划
标准凸规划(DCP)是一种从给定的基本函数库构造已知曲率的数学表达式的系统。CVXPY使用DCP来确保指定的优化问题是凸的。
本教程的这一部分解释了DCP的规则以及CVXPY如何应用这些规则。
访问 dcp.stanford.edu 来获得关于DCP更丰富的互动介绍。
表达式
在CVXPY中,表达式由变量、参数、Python浮点数和Numpy矩阵等数值常量、标准的算术运算符 +, -, *, /, @ 以及一组库函数 原子函数 构成。下面是一些CVXPY表达式的例子:
import cvxpy as cp
# 创建变量和参数。
x, y = cp.Variable(), cp.Variable()
a, b = cp.Parameter(), cp.Parameter()
# CVXPY表达式示例
3.69 + b/3
x - 4*a
sqrt(x) - minimum(y, x - a)
maximum(2.66 - sqrt(y), square(x + 2*y))
表达式可以是标量、向量或矩阵。表达式的维度存储在 expr.shape 中。
总条目数由 expr.size 给出,
而维度数量由 expr.ndim 给出。
如果一个表达式在其维度上的使用方式是不合理的,例如相加不同大小的矩阵,CVXPY会引发异常。
在算术运算中,形状的行为语义与NumPy的ndarray相同(除了某些广播是禁止的)。
import numpy
X = cp.Variable((5, 4))
A = numpy.ones((3, 5))
# 使用expr.shape获取维度信息。
print("dimensions of X:", X.shape)
print("size of X:", X.size)
print("number of dimensions:", X.ndim)
print("dimensions of sum(X):", cp.sum(X).shape)
print("dimensions of A @ X:", (A @ X).shape)
# 无效维度引发ValueError异常。
try:
A + X
except ValueError, e:
print(e)
dimensions of X: (5, 4)
size of X: 20
number of dimensions: 2
dimensions of sum(X): ()
dimensions of A @ X: (3, 4)
Cannot broadcast dimensions (3, 5) (5, 4)
CVXPY使用DCP分析来确定每个表情的符号和曲率。
符号
每个(子)表达式被标记为 正数 (非负)、 负数 (非正)、 零 或 未知 。
较大表达式的符号由其子表达式的符号确定。例如,表达式 expr1*expr2 的符号是:
如果任一表达式的符号为零,则为零。
如果expr1和expr2具有相同(已知)的符号,则为正数。
如果expr1和expr2具有相反(已知)的符号,则为负数。
如果任一表达式的符号未知,则为未知。
赋予表达式的符号始终是正确的。但是DCP符号分析可能会将一个表达式标记为未知符号,即使通过更复杂的分析也可以确定其符号。例如, x*x 是正数,但根据上述规则其符号是未知的。
CVXPY通过查看常数的值来确定其符号。对于标量常数,这是直接的。具有所有正(负)条目的向量和矩阵常数被标记为正(负)。具有正和负条目的向量和矩阵常数被标记为符号未知。
表达式的符号存储在 expr.sign 中:
x = cp.Variable()
a = cp.Parameter(nonpos=True)
c = numpy.array([1, -1])
print("sign of x:", x.sign)
print("sign of a:", a.sign)
print("sign of square(x):", cp.square(x).sign)
print("sign of c*a:", (c*a).sign)
sign of x: UNKNOWN
sign of a: NONPOSITIVE
sign of square(x): NONNEGATIVE
sign of c*a: UNKNOWN
曲率
每个(子)表达式都被标记为以下曲率之一(与其变量相关)
曲率 |
意义 |
|---|---|
constant |
\(f(x)\) 独立于 \(x\) |
affine |
\(f(\theta x + (1-\theta)y) = \theta f(x) + (1-\theta)f(y), \; \forall x, \; y,\; \theta \in [0,1]\) |
convex |
\(f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y), \; \forall x, \; y,\; \theta \in [0,1]\) |
concave |
\(f(\theta x + (1-\theta)y) \geq \theta f(x) + (1-\theta)f(y), \; \forall x, \; y,\; \theta \in [0,1]\) |
unknown |
DCP 分析无法确定曲率 |
使用下面的曲率规则。与符号分析一样,结论总是正确的,但是简单分析会将表达式标记为未知,即使它们是凸的或凹的。请注意,任何常量表达式也是仿射的,并且任何仿射表达式既是凸的又是凹的。
曲率规则
DCP 分析基于将凸分析的一般复合定理应用于每个(子)表达式。
\(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) 是凸的,如果 \(\text{ } f\) 是一个凸函数,并且对于每个 \(\text{expr}_{i}\) ,以下条件之一成立:
\(f\) 在参数 \(i\) 上递增,且 \(\text{expr}_{i}\) 是凸的。
\(f\) 在参数 \(i\) 上递减,且 \(\text{expr}_{i}\) 是凹的。
\(\text{expr}_{i}\) 是仿射的或者常数。
如果 \(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) 是凹的,那么 \(\text{ } f\) 是凹函数,并且对于每个 \(\text{expr}_{i}\) ,满足以下条件之一:
\(f\) 在参数 \(i\) 上递增,且 \(\text{expr}_{i}\) 是凹的。
\(f\) 在参数 \(i\) 上递减,且 \(\text{expr}_{i}\) 是凸的。
\(\text{expr}_{i}\) 是仿射的或者常数。
如果 \(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) 是仿射的,那么 \(\text{ } f\) 是仿射函数,并且每个 \(\text{expr}_{i}\) 都是仿射的。
如果以上三个规则都不适用,表达式 \(f(\text{expr}_1, \text{expr}_2, ..., \text{expr}_n)\) 的曲率被标记为未知。
一个函数在一个参数上的递增或递减取决于该参数的符号。例如,对于正参数, square 是递增的,而对于负参数,它是递减的。
表达式的曲率被存储为 expr.curvature :
x = cp.Variable()
a = cp.Parameter(nonneg=True)
print("curvature of x:", x.curvature)
print("curvature of a:", a.curvature)
print("curvature of square(x):", cp.square(x).curvature)
print("curvature of sqrt(x):", cp.sqrt(x).curvature)
curvature of x: AFFINE
curvature of a: CONSTANT
curvature of square(x): CONVEX
curvature of sqrt(x): CONCAVE
中缀运算符
中缀运算符 +, -, *, / 和矩阵乘法 @ 被视为函数。
中缀运算符 + 和 - 是仿射的,因此上述规则用于标记曲率。例如,如果 expr1 和 expr2 是凸的,expr1 + expr2 就被标记为凸。
expr1*expr2 、 expr1/expr2 和 expr1@expr2
只有在其中一个表达式是常量时才能是DCP。上面的曲率规则适用。例如,当 expr1 是凹的且 expr2 是负且常量时,expr1/expr2 是凸的。
示例 1
DCP分析将表达式分解为子表达式。下面的树形可视化图展示了如何对表达式 2*square(x) + 3 进行操作。每个子表达式显示在蓝色框中。我们在左侧标记其曲率,在右侧标记其符号。
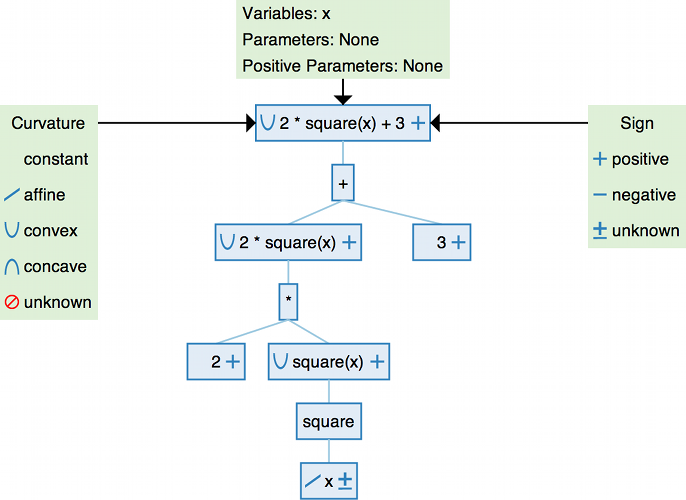
示例 2
我们将分步介绍DCP规则在表达式 sqrt(1 + square(x)) 中的应用。
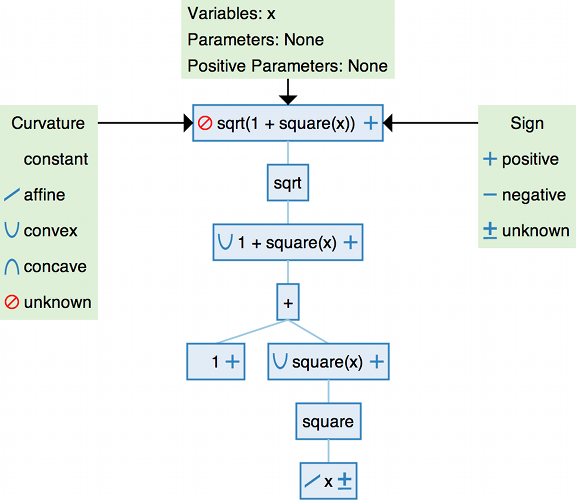
变量 x 具有仿射曲率和未知符号。函数 square 对于未知符号的参数而言是凸函数且非单调的。
它可以接受仿射表达式 x 作为参数;结果 square(x) 是凸函数。
算术运算符 + 是仿射且递增的,因此由凸函数的曲率规则可知,复合函数 1 + square(x) 是凸函数。
函数 sqrt 是凹且递增的,这意味着它只能取凹参数。由于 1 + square(x) 是凸函数,
sqrt(1 + square(x)) 违反了 DCP 规则,无法被验证为凸函数。
实际上, sqrt(1 + square(x)) 是关于 x 的凸函数,但是 DCP 规则无法验证凸性。
如果将表达式写为 norm(hstack(1, x), 2) ,向量 \([1,x]\) 的L2范数,它与 sqrt(1 + square(x)) 具有相同的值,那么它将通过 DCP 规则得到认证,被视为凸函数。
print("sqrt(1 + square(x)) curvature:",
cp.sqrt(1 + cp.square(x)).curvature)
print("norm(hstack([1, x]), 2) curvature:",
cp.norm(cp.hstack([1, x]), 2).curvature)
sqrt(1 + square(x)) curvature: UNKNOWN
norm(hstack(1, x), 2) curvature: CONVEX
DCP 问题
问题由一个目标函数和一系列约束条件构成。如果一个问题符合 DCP 规则,则它保证是凸的并能够被 CVXPY 求解。 DCP 规则要求问题目标函数具有以下两种形式之一:
最小化(凸)
最大化(凹)
在 DCP 规则下,只有以下约束是有效的:
仿射等于仿射
凸小于等于凹
凹大于等于凸
通过调用 object.is_dcp() ,您可以检查问题、约束或目标函数是否符合 DCP 规则。以下是一些 DCP 和非 DCP 问题的示例:
x = cp.Variable()
y = cp.Variable()
# DCP 问题。
prob1 = cp.Problem(cp.Minimize(cp.square(x - y)),
[x + y >= 0])
prob2 = cp.Problem(cp.Maximize(cp.sqrt(x - y)),
[2*x - 3 == y,
cp.square(x) <= 2])
print("prob1 is DCP:", prob1.is_dcp())
print("prob2 is DCP:", prob2.is_dcp())
# 非 DCP 问题。
# 非 DCP 目标函数。
obj = cp.Maximize(cp.square(x))
prob3 = cp.Problem(obj)
print("prob3 is DCP:", prob3.is_dcp())
print("Maximize(square(x)) is DCP:", obj.is_dcp())
# 一个非DCP约束。
prob4 = cp.Problem(cp.Minimize(cp.square(x)),
[cp.sqrt(x) <= 2])
print(f"prob4 is DCP: {prob4.is_dcp()}")
print(f"sqrt(x) <= 2 is DCP: {(cp.sqrt(x) <= 2).is_dcp()}")
prob1 is DCP: True
prob2 is DCP: True
prob3 is DCP: False
Maximize(square(x)) is DCP: False
prob4 is DCP: False
sqrt(x) <= 2 is DCP: False
如果在一个非DCP问题上调用 problem.solve() ,CVXPY会引发异常。
# 一个非DCP问题。
prob = cp.Problem(cp.Minimize(cp.sqrt(x)))
try:
prob.solve()
except Exception as e:
print(e)
问题没有遵循 DCP 规则。