通过凸优化进行航天器设计

考虑一个三角形或楔形的超音速流场中。一个典型的航天器设计优化问题是设计楔形以最大化升阻比（L/D）（或相应地最小化 D/L 比），满足一定的几何约束。在这个例子中，楔形的斜边是恒定的，我们的任务是选择其宽度和高度。

阻力对升力比定义如下：

\[\frac{\mathrm{D}}{\mathrm{L}} = \frac{\mathrm{c_d}}{\mathrm{c_l}},\]

其中 \(\mathrm{c_d}\) 和 \(\mathrm{c_l}\) 分别是阻力和升力系数，通过对与机身平行和垂直方向的压力系数投影进行积分得到。

事实证明，阻力对升力比是一个拟线性函数，我们现在来证明。我们将假设压力系数采用船身擦湿区域的牛顿正弦平方定律，

\[\mathrm{c_p} = 2(\hat{v}\cdot\hat{n})^2\]

在其他地方 \(\mathrm{c_p} = 0\)。这里，\(\hat{v}\) 是自由流方向，为了简化起见，我们假设它与机身平行，即 \(\hat{v} = \langle 1, 0 \rangle\)，而 \(\hat{n}\) 是局部单位法线。对于一个由宽度 \(\Delta x\) 和高度 \(\Delta y\) 定义的楔形，.. math:

\hat{n} = \langle -\Delta y/s,-\Delta x/s \rangle

其中 \(s\) 是斜边的长度。因此，

\[\mathrm{c_p} = 2((1)(-\Delta y/s)+(0)(-\Delta x/s))^2 = \frac{2 \Delta y^2}{s^2}\]

升力和阻力系数由以下公式给出：

\[\begin{split}\begin{align*} \mathrm{c_d} &= \frac{1}{c}\int_0^s -\mathrm{c_p}\hat{n}_x \mathrm{d}s \\ \mathrm{c_l} &= \frac{1}{c}\int_0^s -\mathrm{c_p}\hat{n}_y \mathrm{d}s \end{align*}\end{split}\]

其中 \(c\) 是体的参考弦长。鉴于 \(\hat{n}\) 和 \(\mathrm{c_p}\) 在体的表面上保持不变，

\[\begin{split}\begin{align*} \mathrm{c_d} &= -\frac{s}{c}\mathrm{c_p}\hat{n}_x = \frac{s}{c}\frac{2 \Delta y^2}{s^2}\frac{\Delta y}{s} \\ \mathrm{c_l} &= -\frac{s}{c}\mathrm{c_p}\hat{n}_y = \frac{s}{c}\frac{2 \Delta y^2}{s^2}\frac{\Delta x}{s} \end{align*}\end{split}\]

假设 \(s=1\)，那么 \(\Delta y = \sqrt{1-\Delta x^2}\)， 将上述代入 \(D/L\) 的方程中，我们得到

\[\frac{\mathrm{D}}{\mathrm{L}} = \frac{\Delta y}{\Delta x} = \frac{\sqrt{1-\Delta x^2}}{\Delta x} = \sqrt{\frac{1}{\Delta x^2}-1}.\]

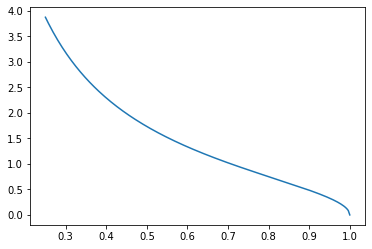
这个函数可以表示为 DQCP（准线性代数方程求解器） 的形式。我们绘制了下面的图表，然后使用 DQCP 进行了编写。

%matplotlib inline

import matplotlib
import numpy as np
import matplotlib.pyplot as plt
import math

x = np.linspace(.25,1,num=201)
obj = []
for i in range(len(x)):
    obj.append(math.sqrt(1/x[i]**2-1))

plt.plot(x,obj)

[<matplotlib.lines.Line2D at 0x7f571d7bfdd8>]

import cvxpy as cp

x = cp.Variable(pos=True)
obj = cp.sqrt(cp.inv_pos(cp.square(x))-1)
print("目标函数是", obj.curvature)

目标函数是QUASILINEAR

将这个目标函数最小化，同时满足代表有效载荷要求的约束条件，是一个标准的航空航天设计问题。在这个问题中，我们考虑楔形体必须能够内部包含一个给定长度和宽度的矩形沿其斜边。这可以表示为一个凸约束条件。

a = .05 # 用户输入：矩形的高度，应小于等于 b
b = .65 # 用户输入：矩形的宽度
constraint = [a*cp.inv_pos(x)-(1-b)*cp.sqrt(1-cp.square(x))<=0]
print(constraint)

[Inequality(Expression(CONVEX, UNKNOWN, ()))]

prob = cp.Problem(cp.Minimize(obj), constraint)
prob.solve(qcp=True, verbose=True)
print('Final L/D Ratio = ', 1/obj.value)
print('Final width of wedge = ', x.value)
print('Final height of wedge = ', math.sqrt(1-x.value**2))

****************************************************************************
正在准备对问题进行二分法划分

最小化 0.0
受限于 0.05 * var30766 + -0.35 * var30793 <= 0.0
           SOC (reshape (var30747 + var30766, (1,)), Vstack (reshape (var30747 + -var30766, (1, 1)), reshape(2.0 * 1.0, (1, 1)) ))
           SOC (reshape (var30779 + 1.0, (1,)), Vstack (reshape (var30779 + -1.0, (1, 1)), reshape(2.0 * var30747, (1, 1)) ))
           SOC (reshape (1.0 + -var30779 + 1.0, (1,)), Vstack (reshape (1.0 + -var30779 + -1.0, (1, 1)), reshape(2.0 * var30793, (1, 1)) ))
           power(power(power(param30811, 2) + --1.0, -1), 1/2) <= var30747

正在查找二分法的间隔 ...
初始下界: 0.000000
初始上界: 1.000000

(迭代 0) 下界: 0.000000
(迭代 0) 上界: 1.000000
(迭代 0) 查询点: 0.500000
(迭代 0) 查询结果是可行的。解决方案 (状态=最优, 目标值=0.0, 原始变量={30766: array(1.28425055), 30793: array(0.32048066), 30747: 0.9203698369509382, 30779: array(0.86287821)}, 对偶变量={30764: 1.184352986830617e-10, 30775: array([ 7.68139086e-12, -9.11799720e-13, -6.85059567e-12]), 30788: array([ 6.73308751e-11,  7.50722737e-12, -6.55220021e-11]), 30802: array([ 4.04979217e-11,  3.43109122e-11, -1.68754271e-11]), 30835: 1.4165742899966837e-10}, 属性={'solve_time': 6.0109e-05, 'setup_time': 4.4997e-05, 'num_iters': 7}))

(迭代 5) 下界: 0.125000
(迭代 5) 上界: 0.156250
(迭代 5) 查询点: 0.140625
(迭代 5) 查询结果是不可行的。

(迭代 10) 下界: 0.145508
(迭代 10) 上界: 0.146484
(迭代 10) 查询点: 0.145996
(迭代 10) 查询结果是可行的。解决方案 (状态=最优, 目标值=0.0, 原始变量={30766: array(1.01067238), 30793: array(0.14440604), 30747: 0.9895144829793, 30779: array(0.97914383)}, 对偶变量={30764: 1.2610785752467482e-05, 30775: array([ 6.37367039e-07,  6.73702792e-09, -6.37322961e-07]), 30788: array([ 1.50627898e-05,  1.58286953e-07, -1.50619494e-05]), 30802: array([ 7.77053008e-06,  7.45051237e-06, -2.20683981e-06]), 30835: 2.948014872712083e-05}, 属性={'solve_time': 0.000114922, 'setup_time': 3.6457e-05, 'num_iters': 10}))

(迭代 15) 下界: 0.145874
(迭代 15) 上界: 0.145905
(迭代 15) 查询点: 0.145889
(迭代 15) 查询结果是不可行的。

二分法已完成，下界为 0.145897，上界为 0.1458979
****************************************************************************

最终的L/D比 =  6.854107648695203
最终楔形体的宽度 =  0.9895238539767502
最终楔形体的高度 =  0.14436946495363565

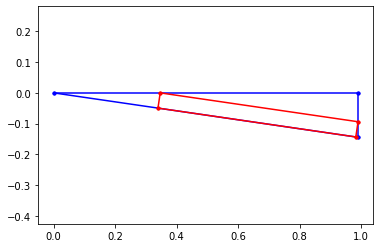
一旦找到解决方案，我们可以创建一个图来验证矩形是否包含在楔形体内。

y = math.sqrt(1-x.value**2)
lambda1 = a*x.value/y
lambda2 = a*x.value**2/y+a*y
lambda3 = a*x.value-y*(a*x.value/y-b)

plt.plot([0,x.value],[0,0],'b.-')
plt.plot([0,x.value],[0,-y],'b.-')
plt.plot([x.value,x.value],[0,-y],'b.-')

pt1 = [lambda1*x.value,-lambda1*y]
pt2 = [(lambda1+b)*x.value,-(lambda1+b)*y]
pt3 = [(lambda1+b)*x.value+a*y,-(lambda1+b)*y+a*x.value]
pt4 = [lambda1*x.value+a*y,-lambda1*y+a*x.value]

plt.plot([pt1[0],pt2[0]],[pt1[1],pt2[1]],'r.-')
plt.plot([pt2[0],pt3[0]],[pt2[1],pt3[1]],'r.-')
plt.plot([pt3[0],pt4[0]],[pt3[1],pt4[1]],'r.-')
plt.plot([pt4[0],pt1[0]],[pt4[1],pt1[1]],'r.-')

plt.axis('equal')

(-0.04947620645689951,
 1.0390003355948896,
 -0.15158793820131744,
 0.0072184732476817896)