分数优化

本文档展示了如何解决一个简单的*凹分数问题*，目标是最大化一个非负凹函数和一个正凸函数的比值。凹分数问题是拟凸规划问题(QCPs)。可以使用 `DQCP <https://www.cvxpy.org/tutorial/dqcp/index.html>`__来指定凹分数问题，并且可以使用CVXPY求解。

!pip install --upgrade cvxpy

import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

我们的目标是最大化函数

\[\frac{\sqrt{x}}{\exp(x)}.\]

这个函数不是凹的，但是它是拟凹的，可以通过观察它的图形来看出。

plt.plot([np.sqrt(y) / np.exp(y) for y in np.linspace(0, 10)])
plt.show()

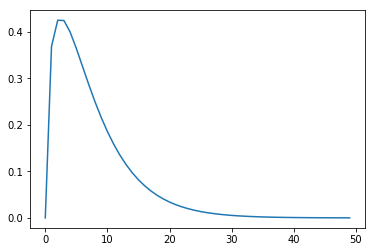
以下代码指定并求解了 QCP，使用了 DQCP。凹函数 DQCP 兼容，因为比值原子在分子为正时随分母增加而增加，在分子为非负时随分母减少。

x = cp.Variable()
concave_fractional_fn = cp.sqrt(x) / cp.exp(x)
problem = cp.Problem(cp.Maximize(concave_fractional_fn))
assert problem.is_dqcp()
problem.solve(qcp=True)

0.4288821220397949

x.value

array(0.50000165)