水灌顶高频通信
作者:罗伯特·高尔斯,罗杰·希尔,萨米·阿利齐,蒂莫西·波林顿和基思·布里格斯
引用自 Boyd 和 Vandenberghe 的《凸优化》,例子 5.2,第 145 页
凸优化可以用来解决经典的水灌顶问题。这个问题是指将总功率 \(P\) 分配给 \(n\) 个通信信道,目标是最大化总通信速率。第 \(i\) 个通道的通信速率由以下公式给出:
\(\log(\alpha_i + x_i)\)
其中 \(x_i\) 表示分配给通道 \(i\) 的功率,\(\alpha_i\) 表示可以向通道添加功率的基线以上的楼层。由于 \(-\log(X)\) 是凸的,我们可以将水灌顶问题转化为凸优化问题:
最小化 \(\sum_{i=1}^N -\log(\alpha_i + x_i)\)
满足 \(x_i \succeq 0\) 和 \(\sum_{i=1}^N x_i = P\)
这种形式也非常容易转化为 DCP 格式,并可以简单地使用 CVXPY 进行求解。
#!/usr/bin/env python3
# @author: R. Gowers, S. Al-Izzi, T. Pollington, R. Hill & K. Briggs
import numpy as np
import cvxpy as cp
def water_filling(n, a, sum_x=1):
'''
Boyd 和 Vandenberghe 的《凸优化》示例 5.2 第 145 页
水填充。
该问题出现在信息论中,用于在一组 n 个通信信道中分配功率,以最大化总信道容量。
变量 x_i 表示分配给第 i 个信道的发射功率,log(α_i+x_i) 给出信道的容量或最大通信速率。
目标是最小化 -∑log(α_i+x_i),在约束条件 ∑x_i = 1 下
'''
# 声明变量和参数
x = cp.Variable(shape=n)
alpha = cp.Parameter(n, nonneg=True)
alpha.value = a
# 选择目标函数。解释为最大化所有信道的总通信速率
obj = cp.Maximize(cp.sum(cp.log(alpha + x)))
# 声明约束条件
constraints = [x >= 0, cp.sum(x) - sum_x == 0]
# 求解
prob = cp.Problem(obj, constraints)
prob.solve()
if(prob.status=='optimal'):
return prob.status, prob.value, x.value
else:
return prob.status, np.nan, np.nan
示例
作为一个简单的示例,我们设定 \(N = 3\),\(P = 1\) 和 \(\boldsymbol{\alpha} = (0.8,1.0,1.2)\)。
该函数输出问题状态、最大通信速率和所需的功率分配是否达到了该最大通信速率。
# 作为示例,我们将解决具有 3 个桶、每个桶具有不同 α 的水填充问题
np.set_printoptions(precision=3)
buckets = 3
alpha = np.array([0.8, 1.0, 1.2])
stat, prob, x = water_filling(buckets, alpha)
print('Problem status: {}'.format(stat))
print('Optimal communication rate = {:.4g} '.format(prob))
print('Transmitter powers:\n{}'.format(x))
Problem status: optimal
Optimal communication rate = 0.863
Transmitter powers:
[0.533 0.333 0.133]
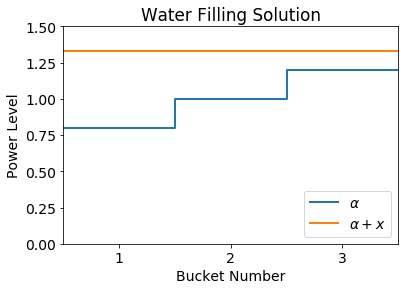
为了说明水注入原理,我们将绘制 \(\alpha_i + x_i\) ,并检查分配功率的地方是否平坦:
import matplotlib
import matplotlib.pylab as plt
%matplotlib inline
matplotlib.rcParams.update({'font.size': 14})
axis = np.arange(0.5,buckets+1.5,1)
index = axis+0.5
X = x.copy()
Y = alpha + X
# to include the last data point as a step, we need to repeat it
A = np.concatenate((alpha,[alpha[-1]]))
X = np.concatenate((X,[X[-1]]))
Y = np.concatenate((Y,[Y[-1]]))
plt.xticks(index)
plt.xlim(0.5,buckets+0.5)
plt.ylim(0,1.5)
plt.step(axis,A,where='post',label =r'$\alpha$',lw=2)
plt.step(axis,Y,where='post',label=r'$\alpha + x$',lw=2)
plt.legend(loc='lower right')
plt.xlabel('Bucket Number')
plt.ylabel('Power Level')
plt.title('Water Filling Solution')
plt.show()