计算线性不等式集合的稀疏解

由Judson Wilson于2014年5月11日进行的衍生作品。改编自Almir Mutapcic于2006年2月28日的同名CVX示例。

主题参考：

  • Boyd＆Vandenberghe的第6.2节“凸优化”

      1. Tropp的“Just relax: Convex programming methods for subset selection and sparse approximation”

介绍

我们考虑一组可行的线性不等式 \(Ax \preceq b\)。我们采用两种启发式方法来寻找满足这些不等式的稀疏点 \(x\)。

寻找稀疏解的（标准） \(\ell_1\)-范数启发式方法为：

\[\begin{split}\begin{array}{ll} \mbox{minimize} & \|x\|_1 \\ \mbox{subject to} & Ax \preceq b. \end{array}\end{split}\]

基于对数的启发式方法是一种迭代方法，用于寻找稀疏解，通过找到问题的局部最优点：.. math:

\begin{array}{ll}
    \mbox{最小化}   &  \sum_i \log \left( \delta + \left|x_i\right| \right) \\
    \mbox{满足约束} & Ax \preceq b,
    \end{array}

其中 \(\delta\) 是一个小阈值（用于确定一个值是否接近于零）。我们无法解决这个问题，因为它是一个凹函数的最小化问题，因此不是一个凸问题。然而，我们可以应用一种启发式方法来线性化目标函数，求解并迭代。这变成了一个加权的 \(\ell_1\)-范数启发式算法：

\[\begin{split}\begin{array}{ll} \mbox{minimize} & \sum_i W_i \left|x_i\right| \\ \mbox{subject to} & Ax \preceq b, \end{array}\end{split}\]

其中在每次迭代中，根据以下规则重新调整权重 \(W_i\)：

\[W_i = 1/(\delta + \left|x_i\right|),\]

其中 \(\delta\) 是一个小阈值。

该算法在以下论文中有描述：

  • “An affine scaling methodology for best basis selection” by B. D. Rao and K. Kreutz-Delgado

  • “Portfolio optimization with linear and fixed transaction costs” by M. S. Lobo, M. Fazel, and S. Boyd生成问题数据

import cvxpy as cp
import numpy as np

# 修正随机数生成器以便我们可以重复实验。
np.random.seed(1)

# 我们认为低于这个阈值的元素为零。
delta = 1e-8

# 问题维度（m个不等式在n维空间中）。
m = 100
n = 50

# 构造一组可行的不等式。
# （这个系统对于x0点是可行的。）
A  = np.random.randn(m, n)
x0 = np.random.randn(n)
b  = A.dot(x0) + np.random.random(m)

\(\ell_1\)-范数启发式算法

# 创建变量。
x_l1 = cp.Variable(shape=n)

# 创建约束条件。
constraints = [A*x_l1 <= b]

# 构造目标函数。
obj = cp.Minimize(cp.norm(x_l1, 1))

# 构造并解决问题。
prob = cp.Problem(obj, constraints)
prob.solve()
print("状态: {}".format(prob.status))

# 解的非零元素个数（其基数或多样性）。
nnz_l1 = (np.absolute(x_l1.value) > delta).sum()
print('在R^{}中找到一个可行的x，它有{}个非零元素。'.format(n, nnz_l1))
print("最优目标函数值: {}".format(obj.value))

状态: 最优
在R^50中找到一个可行的x，它有40个非零元素。
最优目标函数值: 28.582394099513873

迭代日志启发式算法

# 进行15次迭代，为每次运行分配变量以保存非零个数（x的基数）。
NUM_RUNS = 15
nnzs_log = np.array(())

# 将W存储为正参数，以便简单修改问题。
W = cp.Parameter(shape=n, nonneg=True);
x_log = cp.Variable(shape=n)

# 初始权重。
W.value = np.ones(n);

# 设置问题。
obj = cp.Minimize( W.T*cp.abs(x_log) ) # 逐元素积的和
constraints = [A*x_log <= b]
prob = cp.Problem(obj, constraints)

# 进行问题的迭代，并解决和更新W。
for k in range(1, NUM_RUNS+1):
    # 解决问题。
    # ECOS求解器在此问题上存在已知的数值问题，所以要强制使用其他求解器。
    prob.solve(solver=cp.CVXOPT)

    # 检查错误。
    if prob.status != cp.OPTIMAL:
        raise Exception("求解器未收敛！")

    # 显示解向量中新的非零个数。
    nnz = (np.absolute(x_log.value) > delta).sum()
    nnzs_log = np.append(nnzs_log, nnz);
    print('迭代{}：在R^{}中找到了一个可行的x，其中非零个数为{}...'.format(k, n, nnz))

    # 逐元素调整权重并重新迭代
    W.value = np.ones(n)/(delta*np.ones(n) + np.absolute(x_log.value))

Iteration 1: Found a feasible x in R^50 with 48 nonzeros...
Iteration 2: Found a feasible x in R^50 with 36 nonzeros...
Iteration 3: Found a feasible x in R^50 with 33 nonzeros...
Iteration 4: Found a feasible x in R^50 with 33 nonzeros...
Iteration 5: Found a feasible x in R^50 with 33 nonzeros...
Iteration 6: Found a feasible x in R^50 with 33 nonzeros...
Iteration 7: Found a feasible x in R^50 with 33 nonzeros...
Iteration 8: Found a feasible x in R^50 with 33 nonzeros...
Iteration 9: Found a feasible x in R^50 with 33 nonzeros...
Iteration 10: Found a feasible x in R^50 with 33 nonzeros...
Iteration 11: Found a feasible x in R^50 with 33 nonzeros...
Iteration 12: Found a feasible x in R^50 with 33 nonzeros...
Iteration 13: Found a feasible x in R^50 with 33 nonzeros...
Iteration 14: Found a feasible x in R^50 with 33 nonzeros...
Iteration 15: Found a feasible x in R^50 with 33 nonzeros...

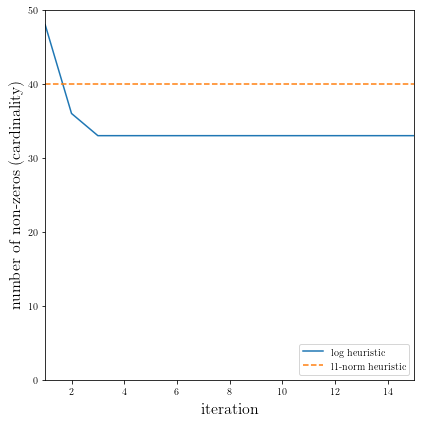
结果绘图

以下代码绘制了:math:ell_1-范数启发式算法的结果，以及每次迭代的log启发式算法的结果。

import matplotlib.pyplot as plt

# 在ipython中内联显示图形。
%matplotlib inline

# 图形属性。
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
plt.figure(figsize=(6,6))

# 绘制两个数据系列。
plt.plot(range(1,1+NUM_RUNS), nnzs_log, label='log启发式算法')
plt.plot((1, NUM_RUNS), (nnz_l1, nnz_l1), linestyle='--', label='l1范数启发式算法')

# 格式化并显示图形。
plt.xlabel('迭代次数', fontsize=16)
plt.ylabel('非零个数（基数）', fontsize=16)
plt.ylim(0,n)
plt.xlim(1,NUM_RUNS)
plt.legend(loc='lower right')

plt.tight_layout()
plt.show()
../../_images/sparse_solution_7_0.png