最佳游行路线
主题参考
迭代加权的 \(\ell_1\) 启发式算法:幻灯片
问题陈述
在这个笔记本中,我们将解决一个问题,即如何在有限数量的卫兵的保护下保护游行路线。
游行路线被离散为 \(m\) 个点。有 \(n\) 个可能的卫兵位置,与决策变量 \(x \in \lbrace 0,1\rbrace^n\) 相关联, 其中 \(x_i = 1\) 当且仅当卫兵被放置在位置 \(i\)。与卫兵位置 \(i\) 相关联的是一个 覆盖向量 \(a_i \in \mathbf{R}^m\), 它描述了位于位置 \(i\) 的卫兵如何”覆盖”游行路线中的每个点。我们假设卫兵覆盖是可加的, 因此描述每个边的总覆盖的向量由 \(Ax\) 给出,其中 \(A \in \mathbf{R}^{m \times n}\) 把 \(a_i\) 作为其 第 \(i\) 列。
游行路线的安全程度取决于覆盖最差的点。我们的目标是放置 \(k\) 个卫兵,以使路线中的点的最小覆盖率最大化。
优化公式
我们可以把这个问题表示为优化问题
松弛
我们可以尝试通过凸优化来处理这个问题,首先形成凸松弛问题
by constraining \(x \in [0,1]^n\).
一般来说,这个问题的解:x:x^star`将具有分数值。由于我们希望得到一个布尔分配,我们可以使用加权:l:ell_1`启发式方法来尝试恢复一个布尔解。
加权:l:ell_1 启发式
为了尝试恢复一个布尔解,我们将解决一系列的凸问题,在每次迭代中将线性项:-w^Tx添加到目标函数中,选择权向量:w:math:w in mathbf{R}^n_+ 来尝试诱导出一个稀疏解向量:x:math:x^star。详细的细节可以在 `Stanford EE364B讲义 <https://stanford.edu/class/ee364b/lectures/l1_ext_slides.pdf>`__中找到。
该算法包括初始化:w:`w = 0`并重复以下两个步骤:
Let \(w_i = \alpha/(\tau + x_i) \forall i\)
until we reach a Boolean solution. Here, \(\alpha\) and \(\tau\) are adjusted to promote a sparse solution. Typical choices would be \(\alpha = 1\) and \(\tau = 10^{-4}\).
Intuitively, the weight vector \(w\) is incentivizing elements of \(x\) which were close to zero in the last iteration towards zero in the next iteration.
示例
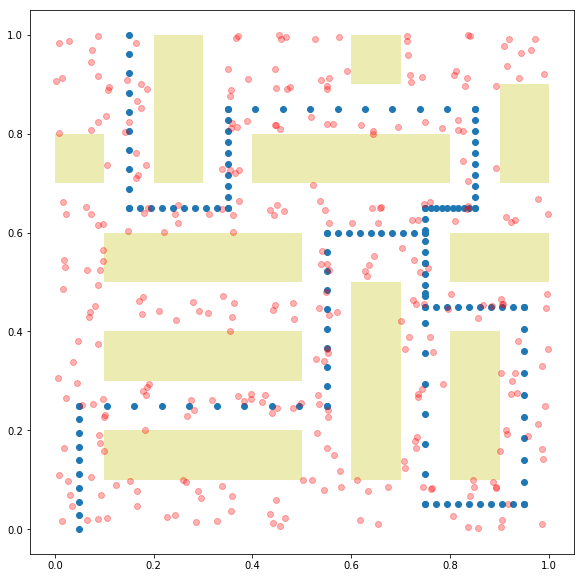
我们在单位正方形 \([0,1] \times [0,1]\) 中创建一个游行路线,通过在连续的线段序列中生成点来实现。 可能的警卫位置是单位正方形中随机放置的点的集合。警卫对游行路线上的点的覆盖是两个点之间的距离的函数。 我们还在单位正方形中添加了建筑物以阻挠警卫的视线。如果警卫的视线被阻挡,他对一个点没有影响。 我们在下面为此问题实例生成 \(A\) 矩阵。
import numpy as np
import matplotlib.pyplot as plt
import cvxpy as cp
def form_path(points,n):
x, y = [], []
pold = points[0]
for p in points[1:]:
x += list(np.linspace(pold[0],p[0],n))
y += list(np.linspace(pold[1],p[1],n))
pold = p
path = np.array([x,y]).T
return path
def form_grid(k):
xs = list(np.linspace(0,1,k))
ys = list(np.linspace(0,1,k))
locations = []
for x in xs:
for y in ys:
locations.append(np.array((x,y)))
return np.array(locations).T
def guard_sets(k,num,noise):
guard_set = []
grid = form_grid(k)
for i in range(num):
pert = noise*np.random.randn(*grid.shape)
guard_set.append( grid+pert )
return np.hstack(guard_set)
def inRect(p,rect):
x,y,w,h = rect
return x <= p[0] and p[0] <= x + w and y <= p[1] and p[1] <= y + h
def remove_guards(guards,buildings):
'''Remove guards inside buildings and outside unit square.'''
outside = []
for i, guard in enumerate(guards.T):
inside = False
for build in buildings:
if inRect(guard,build):
inside = True
break
if not inRect(guard,(0,0,1,1)):
inside = True
break
if not inside:
outside.append(i)
return guards[:,outside]
def intersect(p1,p2,xmin,xmax,ymin,ymax):
'''determine if a rectangle given by xy limits blocks the line of sight between p1 and p2'''
block = False
# if either point inside block
for p in [p1,p1]:
if xmin <= p[0] and p[0] <= xmax and ymin <= p[1] and p[1] <= ymax:
return True
# if the two points are equal at this stage, then they are outside the block
if p1[0] == p2[0] and p1[1] == p2[1]:
return False
if p2[0] != p1[0]:
for x in [xmin,xmax]:
alpha = (x-p1[0])/(p2[0] - p1[0])
y = p1[1] + alpha*(p2[1] - p1[1])
if 0 <= alpha and alpha <= 1 and ymin <= y and y <= ymax:
return True
if p2[1] != p1[1]:
for y in [ymin,ymax]:
alpha = (y-p1[1])/(p2[1] - p1[1])
x = p1[0] + alpha*(p2[0] - p1[0])
if 0 <= alpha and alpha <= 1 and xmin <= x and x <= xmax:
return True
return False
def p_evade(x,y,r=.5,minval=.1):
d = np.linalg.norm(x-y)
if d > r:
return 1
return (1-minval)*d/r + minval
def get_guard_effects(path, guards, buildings, evade_func):
guard_effects = []
for guard in guards.T:
guard_effect = []
for p in path:
prob = 1
if not np.any([intersect(p,guard,x,x+w,y,y+h) for x,y,w,h in buildings]):
prob = evade_func(p,guard)
guard_effect.append(prob)
guard_effects.append(guard_effect)
return np.array(guard_effects).T
locations = []
for x in xs:
for y in ys:
point = np.array((x,y))
detect_p = []
for r in path:
detect_p.append(p_evade(point,r,r=.5,m=0))
locations.append((point,np.array(detect_p)))
np.random.seed(0)
buildings = [(.1,.1,.4,.1),
(.6,.1,.1,.4),
(.1,.3,.4,.1),
(.1,.5,.4,.1),
(.4,.7,.4,.1),
(.8,.1,.1,.3),
(.8,.5,.2,.1),
(.2,.7,.1,.3),
(.0,.7,.1,.1),
(.6,.9,.1,.1),
(.9,.7,.1,.2)]
n = 10
points = [(.05,0),(.05,.25),(.55,.25),(.55,.6),(.75,.6),(.75,.05),(.95,.05), (.95,.45),(.75,.45), (.75,.65),(.85,.65),
(.85,.85),(.35,.85),(.35,.65),(.15,.65),(.15,1)]
path = form_path(points,n)
g = guard_sets(12,4,.02)
g = remove_guards(g,buildings)
guard_effects = get_guard_effects(path, g, buildings, p_evade)
A = 1 - np.log(guard_effects)
fig = plt.figure(figsize=(10,10))
ax = plt.subplot(111,aspect='equal')
for x,y,w,h in buildings:
rect = plt.Rectangle((x,y),w,h,fc='y',alpha=.3)
ax.add_patch(rect)
ax.plot(path[:,0],path[:,1],'o')
ax.plot(g[0,:],g[1,:],'ro',alpha=.3)
[<matplotlib.lines.Line2D at 0x105d17cc0>]
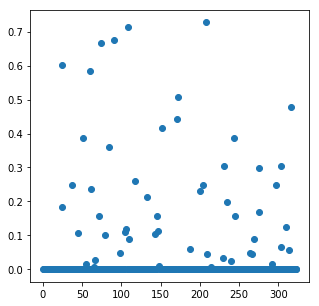
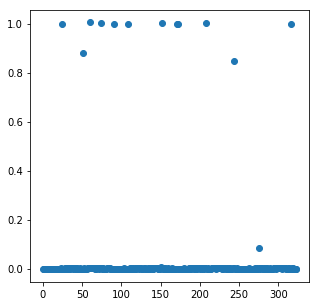
我们执行以下迭代算法。在每一步中,我们绘制向量 \(x\),展示它在每次迭代中变得越来越稀疏。
num_guards = 12
tau = 1e-2
m,n = A.shape
w = np.zeros(n)
for i in range(3):
x = cp.Variable(shape=n)
t = cp.Variable(shape=1)
objective = cp.Maximize(t - x.T*w)
constr = [0 <=x, x <= 1, t <= A*x, cp.sum(x) == num_guards]
cp.Problem(objective, constr).solve(verbose=False)
x = np.array(x.value).flatten()
w = 2/(tau+np.abs(x))
fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(111)
ax.plot(x,'o')
xsol = x
print("final objective value: {}".format(objective.value))
final objective value: -10.27091799207174

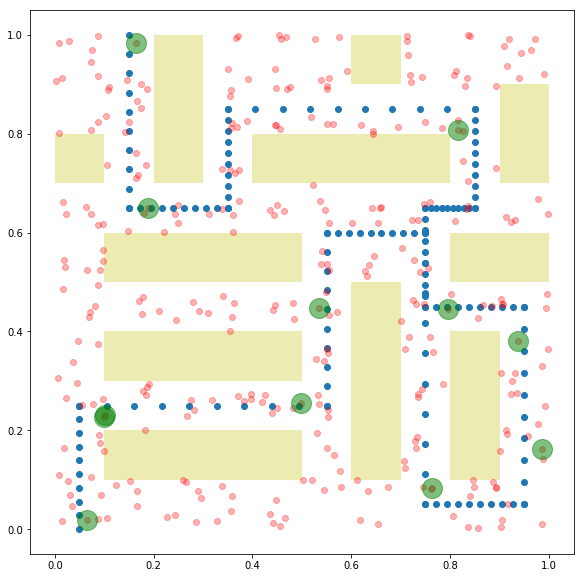
下面,我们绘制了最终的布尔分配图。蓝色点表示游行路线。红色点表示可能的警卫布置位置。绿色点表示实际的警卫布置。黄色矩形是阻挡警卫视线的建筑物。
fig = plt.figure(figsize=(10,10))
ax = plt.subplot(111,aspect='equal')
for x,y,w,h in buildings:
rect = plt.Rectangle((x,y), w, h, fc='y', alpha=.3)
ax.add_patch(rect)
ax.plot(path[:,0], path[:,1], 'o')
ax.plot(g[0,:], g[1,:], 'ro', alpha=.3)
ax.plot(g[0,xsol > .5], g[1,xsol > .5], 'go', markersize=20, alpha=.5)
[<matplotlib.lines.Line2D at 0xb1853f1d0>]