非负矩阵分解

一个由Judson Wilson于2014年6月2日创建的衍生作品。

改编自同名CVX示例，作者为Argyris Zymnis、Joelle Skaf和Stephen Boyd。

介绍

给定矩阵 \(A \in \mathbf{\mbox{R}}^{m \times n}\)，我们希望解决以下问题：

\[\begin{split}\begin{array}{ll} \mbox{最小化} & \| A - YX \|_F \\ \mbox{约束条件} & Y \succeq 0 \\ & X \succeq 0, \end{array}\end{split}\]

其中 \(Y \in \mathbf{\mbox{R}}^{m \times k}\) 和 \(X \in \mathbf{\mbox{R}}^{k \times n}\)。

此示例生成一个随机矩阵 \(A\)，并通过首先生成随机初始猜测 \(Y\) 以及在固定迭代次数内交替最小化 \(X\) 和 \(Y\) 来获得上述问题的*近似*解。

生成问题数据

import cvxpy as cp
import numpy as np

# 确保随机问题数据是可重现的
np.random.seed(0)

# 生成随机数据矩阵 A
m = 10
n = 10
k = 5
A = np.random.rand(m, k).dot(np.random.rand(k, n))

# 随机初始化 Y
Y_init = np.random.rand(m, k)

执行交替最小化

# 确保初始的随机 Y 相同，而不是在每次执行这个单元格时生成新的随机 Y
Y = Y_init

# 执行交替最小化
MAX_ITERS = 30
residual = np.zeros(MAX_ITERS)
for iter_num in range(1, 1+MAX_ITERS):
    # 在迭代开始时，X 和 Y 是 NumPy 数组类型，而不是 CVXPY 变量

    # 对于奇数迭代，保持 Y 不变，优化 X
    if iter_num % 2 == 1:
        X = cp.Variable(shape=(k, n))
        constraint = [X >= 0]
    # 对于偶数迭代，保持 X 不变，优化 Y
    else:
        Y = cp.Variable(shape=(m, k))
        constraint = [Y >= 0]

    # 解决问题
    # 增加最大迭代次数，否则有少数迭代是 "OPTIMAL_INACCURATE"
    # （例如，X 或 Y 中的少数条目在标准公差之外为负数）
    obj = cp.Minimize(cp.norm(A - Y*X, 'fro'))
    prob = cp.Problem(obj, constraint)
    prob.solve(solver=cp.SCS, max_iters=10000)

    if prob.status != cp.OPTIMAL:
        raise Exception("求解器未收敛！")

    print('迭代 {}，残差范数 {}'.format(iter_num, prob.value))
    residual[iter_num-1] = prob.value

    # 将变量转为 NumPy 数组常量供下一次迭代使用
    if iter_num % 2 == 1:
        X = X.value
    else:
        Y = Y.value

迭代 1，残差范数 2.766300564135502
迭代 2，残差范数 0.5840356930600721
迭代 3，残差范数 0.3356679970549085
迭代 4，残差范数 0.18670276027770083
迭代 5，残差范数 0.12819921698143966
迭代 6，残差范数 0.09295501592922492
迭代 7，残差范数 0.06766021043574907
迭代 8，残差范数 0.04958204907945361
迭代 9，残差范数 0.03897402158866238
迭代 10，残差范数 0.02979328283505179
迭代 11，残差范数 0.022938564327729952
迭代 12，残差范数 0.021943924920767337
迭代 13，残差范数 0.01810297853945281
迭代 14，残差范数 0.014551161988556204
迭代 15，残差范数 0.014039687334395924
迭代 16，残差范数 0.009354606824469416
迭代 17，残差范数 0.008643141637584189
迭代 18，残差范数 0.007278100007476402
迭代 19，残差范数 0.008486679700021057
迭代 20，残差范数 0.008827511916396866
迭代 21，残差范数 0.008396764193205366
迭代 22，残差范数 0.005265185332845983
迭代 23，残差范数 0.006931929503816392
迭代 24，残差范数 0.007356156596477946
迭代 25，残差范数 0.0039053948996930054
迭代 26，残差范数 0.003989885269615319
迭代 27，残差范数 0.002920361405226024
迭代 28，残差范数 0.007779246694466739
迭代 29，残差范数 0.007339011292898449
迭代 30，残差范数 0.005008539285258121

输出结果

#
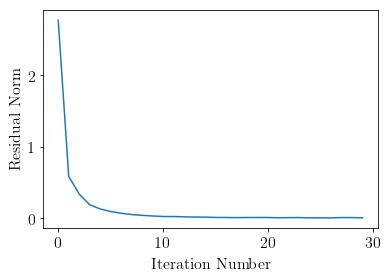
# 绘制残差图。
#

import matplotlib.pyplot as plt

# 在 ipython 中嵌入显示图形。
%matplotlib inline

# 设置绘图属性。
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
font = {'weight' : 'normal',
        'size'   : 16}
plt.rc('font', **font)

# 创建绘图。
plt.plot(residual)
plt.xlabel('迭代次数')
plt.ylabel('残差范数')
plt.show()

#
# 打印结果。
#
print('原始矩阵：')
print(A)
print('左因子 Y：')
print(Y)
print('右因子 X：')
print(X)
print('残差 A - Y * X：')
print(A - Y.dot(X))
print('经过 {} 次迭代的残差：{}'.format(iter_num, prob.value))

原始矩阵：
[[1.323426   1.11061189 1.69137835 1.20020115 1.13216889 0.5980743
  1.64965406 0.340611   1.69871738 0.78278448]
 [1.73721109 1.40464204 1.90898877 1.60774132 1.53717253 0.62647405
  1.76242265 0.41151492 1.8048194  1.20313124]
 [1.4071438  1.10269406 1.75323063 1.18928983 1.23428169 0.60364688
  1.63792853 0.40855006 1.57257432 1.17227344]
 [1.3905141  1.33367163 1.07723947 1.67735654 1.33039096 0.42003169
  1.22641711 0.21470465 1.47350799 0.84931787]
 [1.42153652 1.13598552 2.00816457 1.11463462 1.17914429 0.69942578
  1.90353699 0.45664487 1.81023916 1.09668578]
 [1.60813803 1.23214532 1.73741086 1.3148874  1.27589039 0.40755835
  1.31904948 0.3469129  1.34256526 0.76924618]
 [0.90607895 0.6632877  1.25412229 0.81696721 0.87218892 0.50032884
  1.245879   0.25079329 1.25017792 0.72155621]
 [1.5691922  1.47359672 1.76518996 1.66268312 1.43746574 0.72486628
  1.97409333 0.39239642 2.09234807 1.16325748]
 [1.18723548 1.00282008 1.41532595 1.03836298 0.90382914 0.38460446
  1.213473   0.23641422 1.32784402 0.27179726]
 [0.75789915 0.75119989 0.99502166 0.65444815 0.56073096 0.341146
  1.02555143 0.24273668 1.01035919 0.49427978]]
Left factor Y:
[[ 7.56475742e-01  3.42102372e-01  8.40426641e-01  7.02845111e-01
   4.38002833e-03]
 [ 6.36189366e-01  8.27831861e-01  5.28165827e-01  5.60609403e-01
   3.34595403e-02]
 [ 5.54834858e-01  6.37954560e-01  8.01726231e-01  1.96879041e-01
   3.74736667e-02]
 [ 2.72955779e-01  9.53749151e-01  6.14934798e-02  9.81276972e-01
  -4.26647247e-05]
 [ 7.93952558e-01  3.50946872e-01  1.18853643e+00  3.85961318e-01
   2.96701863e-02]
 [ 7.26183347e-01  4.41639937e-01  2.71711699e-03  7.33393633e-01
   4.55176129e-02]
 [ 4.89263105e-01  4.20725095e-01  7.56036398e-01  6.24033457e-02
  -5.38302416e-04]
 [ 6.09810836e-01  7.55780427e-01  1.03636918e+00  9.08549910e-01
   1.91844947e-03]
 [ 8.31578328e-01  8.75528332e-05  2.93543168e-01  1.10037225e+00
  -2.65884776e-04]
 [ 4.26650967e-01  5.53761974e-02  6.52855369e-01  6.43132832e-01
   1.47569255e-02]]
Right factor X:
[[ 1.07015116e+00  4.25961964e-01  1.59511553e+00  6.26808607e-01
   8.98124301e-01  3.62801718e-01  9.53757673e-01  1.88661317e-01
   9.64559055e-01  1.43675625e-01]
 [ 8.72908811e-01  7.03553498e-01  6.45229205e-01  1.10121868e+00
   9.93621271e-01  3.12383803e-01  7.45085312e-01  1.25155585e-01
   8.84272390e-01  7.94988511e-01]
 [ 1.41086863e-04  1.70049131e-01  2.73427259e-01  2.50933223e-02
   8.38007474e-03  2.51575697e-01  5.99473425e-01  1.39362252e-01
   5.06840502e-01  4.22844259e-01]
 [ 2.70906925e-01  5.46340550e-01  1.04256418e-02  4.63290841e-01
   1.39889787e-01  7.65220031e-03  2.22742919e-01  3.60875098e-02
   3.41601146e-01  2.72448408e-02]
 [ 5.44108256e+00  4.62667224e+00  6.26354249e+00  7.23656013e-01
   1.81220987e+00 -2.57729003e-07  2.90739234e+00  2.81123997e+00
  -2.15606388e-06  6.43189790e+00]]
Residual A - Y * X:
[[ 9.02157264e-04  5.23117764e-04 -5.79950842e-04 -5.74317402e-04
  -4.61768644e-04 -5.28680186e-05  1.62394448e-04  2.76277321e-04
   4.85227596e-04 -5.60481823e-04]
 [-2.33027425e-04  3.21455250e-04  2.17040399e-04  1.56606195e-04
  -2.41256203e-04 -1.01386736e-04  7.36342995e-05 -1.73587325e-05
  -5.22429324e-05 -2.04432888e-04]
 [-8.35846517e-04  2.46121871e-04  5.93720663e-04  5.38806481e-04
  -8.42363429e-05 -1.36215640e-04  2.31633730e-06 -1.52108618e-04
  -3.23620331e-04 -5.42078084e-06]
 [ 2.62860853e-04  1.83780003e-05 -3.20542830e-04 -1.49712163e-04
  -1.31334078e-04  8.78805144e-05  1.46798183e-04 -2.03546983e-05
   4.79256197e-04 -5.81320754e-04]
 [-6.22557723e-04  6.31892711e-04  4.34719938e-04  4.01388769e-04
  -3.52745774e-04 -2.12014739e-04  8.42548761e-05 -4.17321003e-05
  -1.50760383e-04 -3.01455643e-04]
 [-8.46202248e-04  3.61714835e-04  6.15005890e-04  5.85452470e-04
  -2.39872783e-04 -1.59000367e-04  6.24749082e-05 -1.69461803e-04
  -3.16622183e-04 -8.20910778e-05]
 [ 1.15561552e-03 -1.28864368e-03 -1.77288000e-03 -5.10264071e-04
   6.38713553e-04  7.17730381e-04  2.05892579e-04 -2.69449092e-04
   1.71225020e-03 -1.13410340e-03]
 [ 1.57913703e-04  6.21168134e-04 -4.04695033e-05 -1.48187018e-04
  -4.38037868e-04 -1.45409129e-04  1.34145488e-04  1.47289692e-04
   1.98184939e-04 -5.09549810e-04]
 [ 5.51365483e-04 -1.32683206e-03 -1.26345269e-03  6.01647636e-05
   9.72529426e-04  6.10472383e-04 -1.48674297e-05 -3.54468161e-04
   9.92202367e-04 -1.42249517e-04]
 [-1.63514531e-03 -1.59800828e-04  1.08957766e-03  1.01954949e-03
   3.41048252e-04 -1.06257705e-04 -1.57094132e-04 -3.64204427e-04
  -7.26930797e-04  4.63755883e-04]]
Residual after 30 iterations: 0.005008539285258121