待办事项
时间变化的图表
结果表
展示组合数学。为什么不是NP难问题。列举路径。
删除 \(\mathcal{P}\)。用 \(x\) 来描述从开始的路径?
主题参考
加权的迭代 :math:ell_1` 启发法 <http://stanford.edu/class/ee364b/lectures/l1_ext_slides.pdf>`__
分配干扰工作以捕捉走私者
我们将探索一个在图上进行的走私者与安全团队之间的游戏,安全团队试图捕捉走私者。
走私者沿着一个有向图(允许存在循环)移动,图上有 \(n\) 个节点和 \(m\) 条边,从节点 \(0`(起点)到节点 :math:`n-1`(终点)。第 :math:`j\) 条边的逃避概率为 \(p_j\),即走私者在该边上移动而不被察觉的概率。边上的检测事件是独立的,因此走私者到达目的地而未被察觉的概率为 \(\prod_{j \in \mathcal{P}} p_j\),其中 \(\mathcal{P} \subset \lbrace 0,\ldots, m-1\rbrace\) 是走私者路径上的边的集合。我们假设走私者知道逃避概率,并采取使到达终点的概率最大化的路径。
安全团队试图在走私者穿越图时捕捉他。他们可以通过分配资源到边、派遣卫兵等方式来控制图上的逃避概率。现在我们只考虑这个抽象的问题,假设安全团队可以在满足一些约束条件的情况下修改逃避概率。他们的目标是选择逃避概率,以最小化走私者通过而未被察觉的机会。
变换和数学公式的表述
我们对所有概率取对数,以使问题适应凸优化并简化剩余的讨论。这将变量的乘积(通常不是凸的)转换为变量的和(凸的!)。设 \(c_j = \log(p_j)\)。由于这是一一对应关系,当我们谈到“边缘检测概率”时,实际上我们指的是它们的对数,即 \(c\)。这应该根据上下文清楚,并且希望不会引起困惑。
给定 \(c\) 和路径 \(\mathcal{P}\),令 \(P(c, \mathcal{P})\) 为该路径的规避概率的对数。也就是说,
如果 \(\mathcal{P}\) 不是从源到汇的有效路径,则定义 \(P(c, \mathcal{P}) = -\infty\)。我们这样做是为了隐含地编码走私者的路径必须有效的约束条件。
Min/max 游戏
现在我们可以将这个问题解释为一个极小/极大游戏。走私者试图通过选择 \(\mathcal{P}\) 来最大化他逃脱被发现的机会,而安全团队通过选择 \(c\) 来最小化走私者的机会。也就是说,走私者试图最大化 \(P(c, \mathcal{P})\),而安全团队试图最小化它。
我们得到一个具有两个“动作”的游戏。安全团队首先通过选择边缘规避概率 \(c\) 来采取“动作”。走私者在 \(c\) 确定之后再次“动作”(即选择他的路径 \(\mathcal{P}\))。
为了使安全团队能够做出最优的边缘规避概率选择,他们需要模拟走私者在面对任何一组规避概率时会做出什么样的动作。因此,我们将 \(P^\mathrm{opt}(c)\) 定义为问题的最优值
\[ ]:math:P^mathrm{opt}(c) 表示一个最优路径出现时走私者规避(以对数形式表示)的概率,假设他已经知道 \(c\) 的值。
安全团队的目标是在一些对 \(c\) 的约束条件下最小化这个量,我们用集合 \(\mathcal{C}\) 表示。令 \(P^{\star}\) 表示 \(P^\mathrm{opt}(c)\) 的最优值。
在接下来的部分,我们首先研究走私者的目标,以便获得 \(P^\mathrm{opt}(c)\) 的凸形式,并且可以用来分析和优化安全团队的目标。
辅助函数
下面的代码块包含一些用于生成示例和绘制结果的辅助函数。这部分是大部分代码。实际的 CVXPY 优化代码只有几行。我们将在笔记本的后面介绍优化代码。
#%config InlineBackend.figure_format = 'pdf'
#%config InlineBackend.figure_format = 'svg'
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx
import cvxpy as cp
from matplotlib import rcParams
rcParams.update({'font.size': 16})
def formGraph(N,mu,eta,buildings=None,seed=None,dummyNodes=False):
''' Form N by N grid of nodes, perturb by mu and connect nodes within eta.
mu and eta are relative to 1/(N-1)
buildings is a list of tuples (x,y,w,h)
'''
if seed is not None:
np.random.seed(seed)
mu = mu/(N-1)
eta = eta/(N-1)
# generate perterbed grid positions for the nodes
pos = [(i + mu*np.random.randn(), j + mu*np.random.randn())\
for i in np.linspace(0,1,N) for j in np.linspace(1,0,N)]
#select out nodes that end up inside buildings
if buildings is not None and buildings != []:
pos2 = []
for p in pos:
inside = False
for x,y,w,h in buildings:
if x <= p[0] and p[0] <= x + w and y <= p[1] and p[1] <= y + h:
inside = True
break
if not inside:
pos2.append(p)
pos = pos2
# add dummy nodes for multiple entry/exit example
if dummyNodes:
pos = [(-.5,.5)] + pos + [(1.5,.5)]
pos = dict(enumerate(pos))
n = len(pos)
# connect nodes with edges
G = nx.random_geometric_graph(n,eta,pos=pos)
# remove edges that cross buildings
if buildings is not None and buildings != []:
for e in list(G.edges()):
blocked = False
for x,y,w,h in buildings:
if intersect(pos[e[0]],pos[e[1]],x,x+w,y,y+h):
blocked = True
if blocked:
G.remove_edge(*e)
G = nx.DiGraph(G)
# add edges connecting dummy nodes to nodes on left and right edges of grid
if dummyNodes:
for i in range(N):
G.add_edge(0,i+1)
G.add_edge(n-i-2,n-1)
return G, pos
def showPaths(G,pos,edgeProbs=1.0,path=None,visibleNodes=None,Gnodes=None,Rnodes=None,guards=None):
''' Takes directed graph G, node positions pos, and edge probabilities.
Optionally uses path (a list of edge indices) to plot the smuggler's path.
edgeProbd gives the probabilities for all the edges, including hidden ones.
path includes all the edges, including the hidden ones
Gnodes and Rnodes denote the source and destination nodes, to be plotted green
and red respectively.
guards is a list of node indices for denoting guards with a black dot on the plot
'''
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, aspect='equal')
n = G.number_of_nodes()
if visibleNodes is None:
visibleNodes = G.nodes()
# draw the regular interior nodes in the graph
nx.draw_networkx_nodes(G,pos,nodelist=visibleNodes, edgecolors='k',
node_color='w',node_size=100,ax=ax)
# draw the origin and destination nodes
for nodes, color in zip([Gnodes,Rnodes],['g','r']):
for color2, alpha in zip(['w',color],[1,.2]):
nx.draw_networkx_nodes(G,pos,
nodelist=nodes,
node_color=color2,
edgecolors='k',
node_size=200,
ax=ax,alpha=alpha)
# draw guard nodes
if guards is not None:
nx.draw_networkx_nodes(G,pos,nodelist=guards,node_color='k',
node_size=100,ax=ax)
if path is None:
alpha = 1
else:
alpha = .15
# start messing with edges
edge2ind = {e:i for i,e in enumerate(G.edges())}
ind2edge = {i:e for i,e in enumerate(G.edges())}
# only display edges between non-dummy nodes
visibleEdges = [i for i in range(len(edge2ind)) if ind2edge[i][0] in visibleNodes and ind2edge[i][1] in visibleNodes]
edgelist = [ind2edge[i] for i in visibleEdges]
if isinstance(edgeProbs,float):
edgeProbs = [edgeProbs]*G.number_of_edges()
p = [edgeProbs[i] for i in visibleEdges]
# draw edges of graph, make transparent if we're drawing a path over them
edges = nx.draw_networkx_edges(G,pos,edge_color=p,width=4,
edge_cmap=plt.cm.RdYlGn,arrows=False,edgelist=edgelist,edge_vmin=0.0,
edge_vmax=1.0,ax=ax,alpha=alpha)
# draw the path, only between visible nodes
if path is not None:
visiblePath = [i for i in path if ind2edge[i][0] in visibleNodes and ind2edge[i][1] in visibleNodes]
path_pairs = [ind2edge[i] for i in visiblePath]
path_colors = [edgeProbs[i] for i in visiblePath]
edges = nx.draw_networkx_edges(G,pos,edge_color=path_colors,width=8,
edge_cmap=plt.cm.RdYlGn,edgelist=path_pairs,arrows=False,edge_vmin=0.0,
edge_vmax=1.0)
fig.colorbar(edges,label='Evasion probability')
ax.axis([-0.05,1.05,-0.05,1.05])
#ax.axis('tight')
#ax.axis('equal')
ax.axis('off')
return fig, ax
def optPath(G,p):
''' Find the optimal smuggler's path in directed graph G
with edge evasion probabilities p and dictionary
edge2ind bringing node pairs to edge indices
'''
edge2ind = {e:i for i,e in enumerate(G.edges())}
H = G.copy()
p = np.minimum(p,1)
w = -np.log(p)
n = H.number_of_nodes()
for i in H:
for j in H[i]:
H[i][j]['w'] = w[edge2ind[(i,j)]]
path = nx.shortest_path(H,0,n-1,'w')
#path = nx.astar_path(H,0,n-1,weight='w')
foo = [edge2ind[(i,j)] for i,j in zip(path[:-1],path[1:])]
x = np.zeros_like(p)
x[foo] = 1
return x
def intersect(p1,p2,xmin,xmax,ymin,ymax):
'''determine if a rectangle given by xy limits blocks the line of sight between p1 and p2'''
block = False
# if either point inside block
for p in [p1,p1]:
if xmin <= p[0] and p[0] <= xmax and ymin <= p[1] and p[1] <= ymax:
return True
# if the two points are equal at this stage, then they are outside the block
if p1[0] == p2[0] and p1[1] == p2[1]:
return False
if p2[0] != p1[0]:
for x in [xmin,xmax]:
alpha = (x-p1[0])/(p2[0] - p1[0])
y = p1[1] + alpha*(p2[1] - p1[1])
if 0 <= alpha and alpha <= 1 and ymin <= y and y <= ymax:
return True
if p2[1] != p1[1]:
for y in [ymin,ymax]:
alpha = (y-p1[1])/(p2[1] - p1[1])
x = p1[0] + alpha*(p2[0] - p1[0])
if 0 <= alpha and alpha <= 1 and xmin <= x and x <= xmax:
return True
return False
def getGuardEffects(G,pos,guardIdxs,buildings=None,dummyNodes=None):
''' for n guards and m edges, return an m by n matrix giving the
effect of each guard on the evasion probabilities of each edge
in the graph.
Ignore dummy nodes, if any. Guards cannot see through buildings.
guardIdxs is a list of the node indices where we would consider placing
guards
Return the log of the detection probabilities for each guard.
'''
def evadeProb(x,radius=.2):
r = np.linalg.norm(x)/radius
return min(r+.1,1)
m = G.number_of_edges()
if buildings is None:
buildings = []
if dummyNodes is None:
dummyNodes = []
ind2edge = {i:e for i,e in enumerate(G.edges())}
edgeCenters = []
for e in G.edges():
edgeCenters.append((np.array(pos[e[0]]) + np.array(pos[e[1]]))/2)
edgeCenters = np.array(edgeCenters)
numGuards = len(guardIdxs)
edgeVals = np.zeros((m,numGuards))
for i,gid in enumerate(guardIdxs):
for j in range(m):
blocked = False
for x,y,w,h in buildings:
if intersect(edgeCenters[j,:],pos[gid],x,x+w,y,y+h):
blocked = True
break
e = ind2edge[j]
if e[0] in dummyNodes or e[1] in dummyNodes:
blocked = True
if not blocked:
edgeVals[j,i] += np.log(evadeProb(pos[gid]-edgeCenters[j,:],.3))
return edgeVals
def get_a(G,seed=None):
'''
Generate a random value in [0,1] for each edge in the graph.
For directed graphs, directed edges between the same nodes should have the same value
'''
if seed is not None:
np.random.seed(seed)
m = G.number_of_edges()
a = np.zeros((m))
edge2ind = {e:i for i,e in enumerate(G.edges())}
for e in G.edges():
a[edge2ind[e]] = np.random.rand()
e2 = (e[1],e[0])
if e2 in edge2ind:
a[edge2ind[e2]] = a[edge2ind[e]]
return a
Smuggler’s objective
The smuggler chooses a path \(\mathcal{P}\) only after \(c\) is fixed. His goal is to find a valid path in the graph which maximizes \(\sum_{j \in \mathcal{P}} c_j\). Note that this problem can be cast and solved exactly as a shortest path problem in graph theory. We formulate it here as a convex problem so that the security team can use the model to thwart the smuggler.
我们将可能的路径用一个布尔决策变量 \(x \in \lbrace 0,1 \rbrace^m\) 表示,其中 \(x_j = 1\) 表示 \(j \in \mathcal{P}\)。注意这样可以将走私者的目标表达为
变量 \(x\) 需要满足一定的约束条件,以表示一个有效的路径。首先,路径离开源节点的次数必须比进入源节点的次数多一次。类似地,路径进入目标节点的次数必须比离开目标节点的次数多一次。对于图中的其他节点,路径进入和离开节点的次数必须相等。这些约束条件可以表示为 \(Ax = b\),其中
\[ b_i = ]
\[ A_{ij} = ]
走私者问题可以被写成这样,其中 \(P^\mathrm{opt}(c)\) 是问题的最优值
\[ ]
这是一个具有布尔变量的线性问题,不是凸问题,但我们可以通过放宽布尔约束将其转化为一个凸问题,从而得到线性规划问题
\[ ],其最优值为 \(P^{\mathrm{opt}}_\mathrm{R}(c)\)。这个放松的凸问题恰好完全解决了原始的布尔问题。也就是说, \(P^\mathrm{opt}(c) = P^\mathrm{opt}_\mathrm{R}(c)\), 因此我们在余下的部分中只会写 \(P^\mathrm{opt}\)。此外, 如果存在唯一的最优路径,则LP的解 \(x^\star\) 将是布尔型的。 在存在多个最优路径的情况下, \(x^\star\) 可能具有分数条目, 但仍然可以恢复出一个最优路径。
对于安全团队来说,我们只需要知道布尔型和LP型的最优值是相等的。 在继续讨论安全团队的角度之前,我们将看一个例子,了解走私者在给定图中选择最优路径的示例。
走私者路径示例
我们将在一个示例网络上求解走私者问题,以展示最优路径的一个示例。
我们将创建一个大小为 \(N \times N\) 的点网格,加入一些微小扰动以使图形不规则, 如果两个节点之间的距离小于 \(\eta\),则用两条有向边(单向各一条)连接这两个节点。 边对 \((i,j)\) 和 \((j,i)\) 具有相同的躲避概率,即两个连接节点之间的躲避概率是相同的。 躲避概率将是分布在 \(p_j = e^{-a_j}\),其中 \(a_j\) 是均匀分布于区间 \(\left[0,1\right]\) 上的随机变量。
走私者将从图绘制的左上角节点 \(0\) 开始,找到一条到达图绘制右下角节点 \(n-1\) 的最优路径。
我们在下面展示了带有边躲避概率的图示。
N = 10
G, pos = formGraph(N,.12,1.2,seed=5)
n = G.number_of_nodes()
a = get_a(G,seed=2)
p = np.exp(-a)
fig, ax = showPaths(G,pos,p,Gnodes=[0],Rnodes=[n-1])
/anaconda3/envs/cvxpy/lib/python3.6/site-packages/networkx/drawing/nx_pylab.py:611: MatplotlibDeprecationWarning: isinstance(..., numbers.Number)
if cb.is_numlike(alpha):
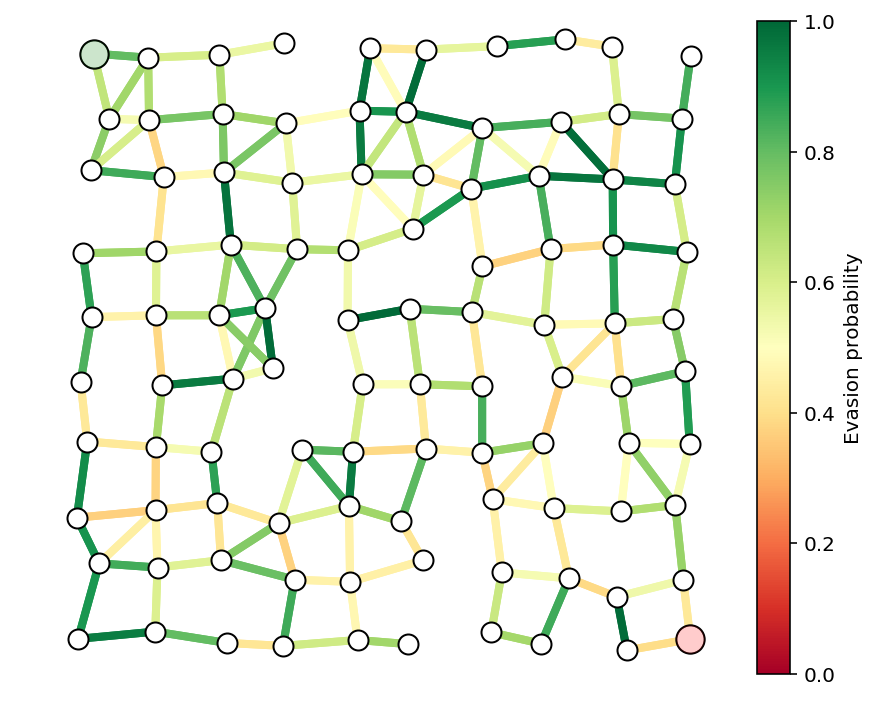
我们构建了走私者的放松凸问题,并解决它以找到他的最佳路径。我们在下面绘制了路径。
A = nx.incidence_matrix(G,oriented=True).toarray()
n,m = A.shape
b = np.zeros(n)
b[0] = -1
b[n-1] = 1
c = np.log(p)
edge2ind = {e: i for i,e in enumerate(G.edges())}
B = np.zeros((int(m/2),m))
count = 0
for i in G:
for j in G[i]:
if i < j:
B[count,edge2ind[(i,j)]] = 1
B[count,edge2ind[(j,i)]] = -1
count += 1
x = cp.Variable(shape=m)
constr = [A*x == b,x>=0, x <= 1]
cp.Problem(cp.Maximize(x.T*c),constr).solve(verbose=True)
x = np.array(x.value).flatten()
-----------------------------------------------------------------
OSQP v0.4.1 - Operator Splitting QP Solver
(c) Bartolomeo Stellato, Goran Banjac
University of Oxford - Stanford University 2018
-----------------------------------------------------------------
problem: variables n = 354, constraints m = 808
nnz(P) + nnz(A) = 1416
settings: linear system solver = qdldl,
eps_abs = 1.0e-03, eps_rel = 1.0e-03,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (adaptive),
sigma = 1.00e-06, alpha = 1.60, max_iter = 4000
check_termination: on (interval 25),
scaling: on, scaled_termination: off
warm start: on, polish: on
iter objective pri res dua res rho time
1 -8.9458e+02 8.00e+00 9.97e+01 1.00e-01 2.10e-03s
75 5.0606e+00 1.47e-03 5.64e-05 1.00e-01 8.35e-03s
status: solved
solution polish: unsuccessful
number of iterations: 75
optimal objective: 5.0606
run time: 1.15e-02s
optimal rho estimate: 5.09e-01
path = list(np.flatnonzero(x > .1))
showPaths(G,pos,p,path,Gnodes=[0],Rnodes=[n-1])
print("The evasion probability of the smuggler's "
"optimal path is %e, or %.3f%%."%(np.exp(x.dot(c)), np.exp(x.dot(c))*100))
The evasion probability of the smuggler's optimal path is 6.341943e-03, or 0.634%.
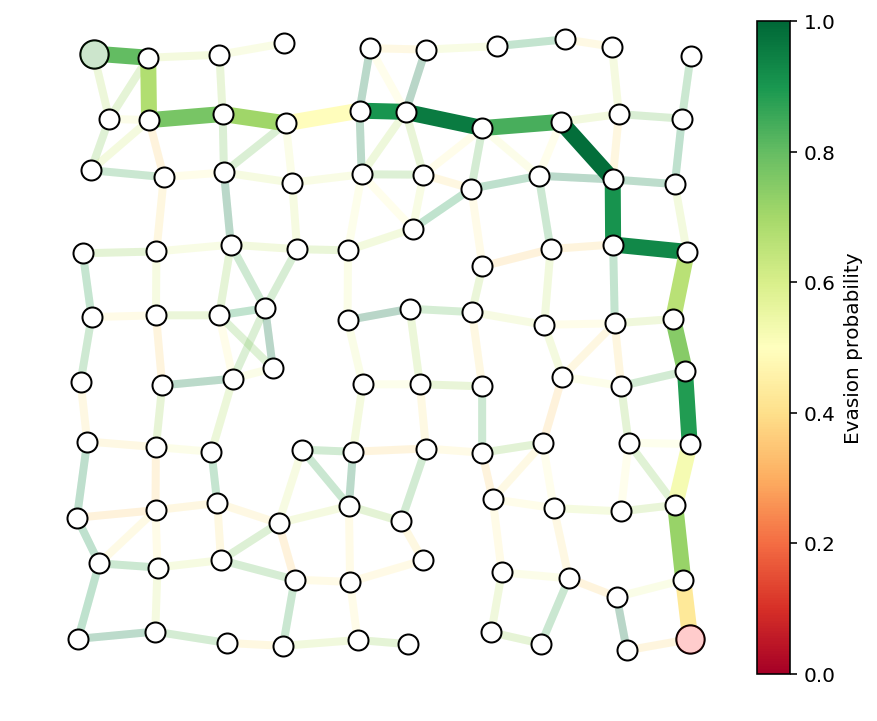
我们在同一个图上运行了一个离散图论最短路径算法,以检查我们是否得到了相同的最优路径。函数``optPath``使用了NetworkX Python包和`Dijkstra算法 <http://en.wikipedia.org/wiki/Dijkstra%27s_algorithm>`__来计算最优路径。
y = optPath(G, p)
path = list(np.flatnonzero(y > .1))
showPaths(G, pos, p, path, Gnodes=[0], Rnodes=[n-1])
print("走私者的最优路径的逃避概率为%e,或%.3f%%。" % (np.exp(y.dot(c)), np.exp(y.dot(c))*100))
走私者的最优路径的逃避概率为6.343747e-03,或0.634%。.. image:: interdiction_files/interdiction_10_1.png
:width: 438px
:height: 360px
安全性目标
安全团队的目标是将 \(P^\mathrm{opt}(c)\) 最小化, 其中 \(c \in \mathcal{C}\) 表示一些约束(比如预算或人员限制):
\[ ]
但请注意, \(P^\mathrm{opt}(c)\) 是问题的最优值:
\[ ]
我们希望将这两个优化问题合并成一个供安全团队解决的单一问题,但是由于一个问题的变量 \(x\) 与另一个问题的变量 \(c\) 相乘,这在一般情况下不是一个凸目标。为了解决这个问题,我们将采用贝叶斯法则的对偶(Convex Optimization 书籍的第五章)。
设 \(D^\mathrm{opt}(c)\) 表示贝叶斯法则的对偶问题的最优值,其中
\[ ] 且 \(\lambda\) 为对偶变量。
对偶理论保证 \(D^\mathrm{opt}(c) = P^\mathrm{opt}(c)\),这使得我们可以将安全团队的问题写成:\[ ]我们可以将其重写为一个优化问题
\[ ]其中 \(c\) 和 \(\lambda\) 是优化变量。
我们将将此问题的最优值表示为 \(P^\star\)。通过求解找到 \(c^\star\),安全团队将能够最优地分配资源,使走私者的探测概率最大化。
安全示例
我们将考虑与上一个示例相同的网络上的安全问题,其中边缘规避概率被建模为 \(p_j = e^{-a_j r_j}\),其中 \(r_j \in \mathbf{R}_+\) 表示分配给边缘 \(j\) 的资源(例如,年度预算)。我们假设 \(a_j \in \mathbf{R}_{++}\) 是已知的,并代表了保护边缘所涉及的成本。与上一个示例一样, \(a_j\) 是一个在区间 \(\left[0,1\right]\) 上的均匀随机变量。
我们将使用与上一个示例相同的随机种子,因此上一个示例对应于当前模型中所有 \(j\) 的特定分配 \(r_j = 1\)。我们将使用这个结果来比较天真的均匀资源分配与最优分配的探测概率。
对于这个示例,我们将施加最大预算约束 \(\sum_{j=0}^{m-1} r_j = m\),以及每个边缘的均匀支出限制 \(r_j \leq R\)。
我们还将约束规避概率在两个方向上相等。也就是说,边缘 \((i,j)\) 和边缘 \((j,i)\) 具有相等的规避概率。我们将使用矩阵 \(B\) 强制执行该约束,其中 \(Br = 0\)。
最终的模型为 \[ ]
我们以 \(R=5\) 解决下面的模型,并报告走私者最优路径的规避概率。.. code:: python
nu = cp.Variable(shape=n) r = cp.Variable(shape=m) constr = [A.T*nu >= -cp.multiply(a,r), cp.sum(r) == m, r >= 0, B*r == 0, r <= 5] cp.Problem(cp.Minimize(nu.T*b),constr).solve(verbose=True) nu = np.array(nu.value).flatten() r = np.array(r.value).flatten()
-----------------------------------------------------------------
OSQP v0.4.1 - 分解QP问题的操作器
(c) Bartolomeo Stellato, Goran Banjac
牛津大学 - 斯坦福大学 2018
-----------------------------------------------------------------
问题: 变量 n = 454, 约束条件 m = 1240
nnz(P) + nnz(A) = 2478
设置: 线性系统解算器 = qdldl,
eps_abs = 1.0e-03, eps_rel = 1.0e-03,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (自适应),
sigma = 1.00e-06, alpha = 1.60, max_iter = 4000
检查终止条件: 打开 (间隔 25),
缩放: 打开, 缩放终止条件: 关闭
加热启动: 打开, 光滑: 打开
迭代 目标 pri 阻滞 dua 阻滞 rho 时间
1 -3.3084e+01 3.54e+02 3.54e+04 1.00e-01 2.59e-03秒
100 -2.2269e+01 3.28e-01 1.58e-03 5.35e-03 9.06e-03秒
状态: 已解
解决方案光滑: 不成功
迭代次数: 100
最优目标值: -22.2692
运行时: 1.05e-02秒
最优的rho估计: 4.10e-03
print("走私者最佳路径的逃避概率为 %e."%(np.exp(nu.dot(b)),))
print("与均匀资源分配相比,走私者的逃避几率减小了 %.2f 倍."%(np.exp(x.dot(c))/np.exp(nu.dot(b))))
走私者最佳路径的逃避概率为 2.131035e-10.
与均匀资源分配相比,走私者的逃避几率减小了 29759913.87 倍。
这里展示了从最优分配结果得到的边缘逃避概率的图表。
showPaths(G,pos,p,Gnodes=[0],Rnodes=[n-1])
图像:
- (<Figure size 576x432 with 2 Axes>,
<matplotlib.axes._subplots.AxesSubplot at 0xd19325278>)
- 
- 宽度:
438px
- 高度:
360px
我们可以使用这些最优资源分配来解决走私者问题,但我们将不能恢复 \(x^{\star}\) 的布尔解,因为最佳路径不唯一。然而,请注意,最佳逃避概率是相同的。
Python代码:
c = np.log(p) x = cp.Variable(shape=m) constr = [A*x == b,x>=0, x <= 1] cp.Problem(cp.Maximize(x.T*c),constr).solve(verbose=True) x = np.array(x.value).flatten()
plt.plot(x) print(“走私者最佳路径的逃避概率为 %e.”%(np.exp(x.dot(c)),))
- ![图像]:—————————————————————–
- OSQP v0.4.1 - 运算分裂二次规划求解器
Bartolomeo Stellato, Goran Banjac
牛津大学 - 斯坦福大学 2018
- 设置:线性系统求解器 = qdldl,
eps_abs = 1.0e-03,eps_rel = 1.0e-03, eps_prim_inf = 1.0e-04,eps_dual_inf = 1.0e-04, rho = 1.00e-01(自适应), sigma = 1.00e-06,alpha = 1.60,max_iter = 4000 check_termination:开启(间隔 25), scaling:开启,scaled_termination:关闭 温启动:开启,polish:开启
- 迭代 目标值 主要残差 对偶残差 rho 时间
1 -8.8977e+02 8.00e+00 4.71e+02 1.00e-01 9.14e-04秒
200 2.0447e+01 7.16e-03 6.89e-03 1.00e-01 6.66e-03秒 325 2.0607e+01 9.79e-04 2.46e-03 1.00e-01 9.95e-03秒
状态: 已解决 解决方案优化: 未成功 迭代次数: 325 最优目标值: 20.6072 运行时间: 1.08e-02秒 最优rho估计: 1.37e-01
走私者最佳路线的回避概率为 1.123036e-09。
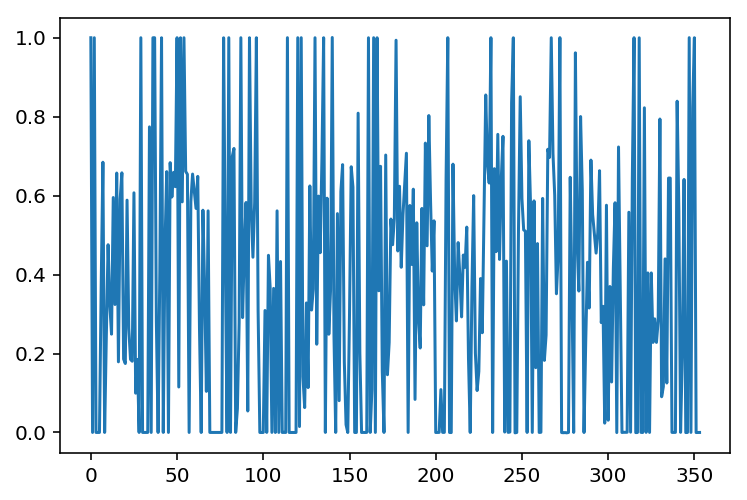
我们再次使用 Dijkstra’s_algorithm 来恢复走私者的最佳路径,以防路径不唯一,并在下面绘制。我们再次检查检测概率是否与之前预测的相符。
x = optPath(G,p)
path = list(np.flatnonzero(x > .1))
showPaths(G,pos,p,path,Gnodes=[0],Rnodes=[n-1])
print("走私者最佳路径的回避概率为 %e."%(np.exp(x.dot(c)),))
走私者最佳路径的回避概率为 9.553365e-10。
现在我们来看一个更高级的例子。
在之前的例子中,安全团队可以直接控制每条边上的回避概率。在本节中,我们将考虑一个例子,安全团队只能通过守卫的部署来控制边的概率,每个守卫会影响到离它较近的边。
在上一个例子中,安全团队在源节点和目标节点附近投入了很多精力。为了让团队的工作变得更加困难,我们将允许走私者的路径可以从图的左侧的任何节点开始,并在图的右侧的任何节点结束。这将迫使团队更平均地分配资源到整个图中。
为了让事情变得更有趣,我们将在图所覆盖的区域中添加”建筑物”。走私者和安全团队将不得不绕过这些建筑物。也就是说,没有节点位于建筑物内部,边也不会穿过建筑物,守卫无法透过建筑物的墙壁看到,这就限制了守卫的视线和其对附近边的影响。
多源点和多目标点
为了允许多个源点和目标点而不改变凸形式,我们将添加一个虚拟源节点和一个虚拟汇节点。虚拟源节点将与图中每个左侧的节点相连。虚拟汇节点将与图中每个右侧的节点相连。我们将确保这些虚拟边的回避概率永远为1。下面的图示说明了这个想法。我们不会绘制虚拟节点或边,但我们将像之前一样用浅绿色和红色突出显示”新的”源节点和汇节点。
# show dummy source and destination node
N = 10
G, pos = formGraph(N,.1,1.2,seed=1,dummyNodes=True)
n = G.number_of_nodes()
fig, ax = showPaths(G,pos,Gnodes=[0],Rnodes=[n-1])
ax.axis([-.6,1.6,-.05,1.05]);.. image:: interdiction_files/interdiction_21_0.png
:width: 469px
:height: 350px
警卫
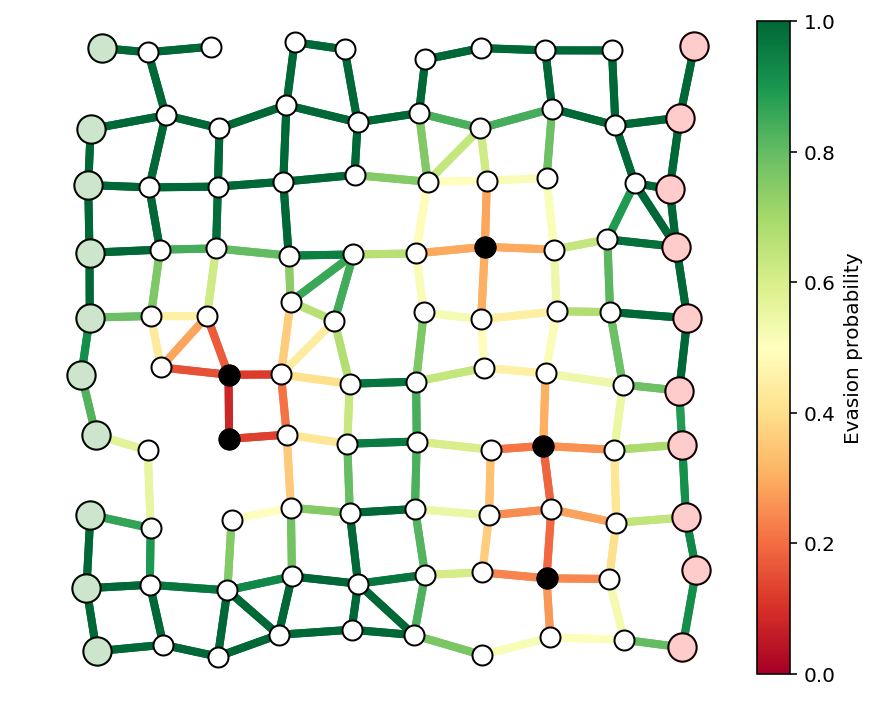
安全团队将选择一部分警卫放置在图中。每个警卫都有一个配置文件,该配置文件给出了他对逃避概率的影响。警卫的影响将取决于他离每条边的中心的距离。原则上,警卫可以放置在图所占据的区域的任何地方,但为了方便可视化,我们只考虑放置在节点位置上的警卫。
下面是几个警卫的示例以及结果逃避概率。
N = 10
k = 5
G, pos = formGraph(N,.1,1.2,seed=3,dummyNodes=True)
n = G.number_of_nodes()
guardIdxs = list(np.random.choice(list(range(N+1,n-N-1)),k,replace=False))
visibleNodes = range(1,n-1)
Gnodes = range(1,N+1)
Rnodes = range(n-2,n-N-2,-1)
edgeVals = getGuardEffects(G,pos,guardIdxs,dummyNodes=[0,n-1])
edgeProbs = edgeVals.sum(axis=1)
edgeProbs = np.exp(edgeProbs)
fig, ax = showPaths(G,pos,edgeProbs,visibleNodes=visibleNodes,Gnodes=Gnodes,Rnodes=Rnodes,guards=guardIdxs)
建筑物
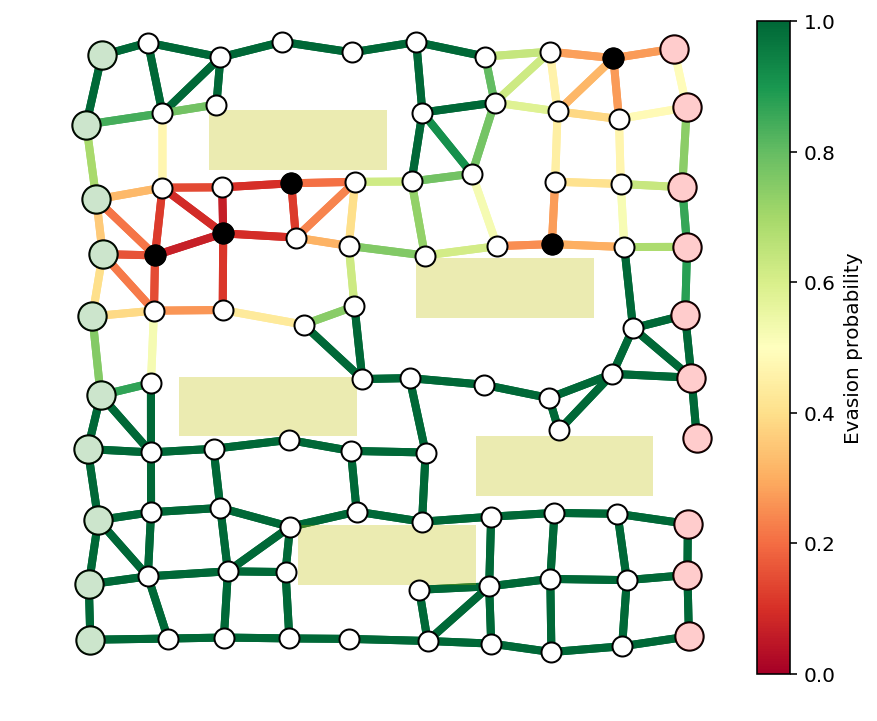
我们还将添加建筑物,它将修改图的拓扑结构,并限制警卫的视野。.. code:: python
N = 10 k = 5 buildings = [(.2,.8,.3,.1),
(.35,.1,.3,.1), (.55,.55,.3,.1), (.15,.35,.3,.1), (.65,.25,.3,.1)]
G, pos = formGraph(N,.11,1.25,buildings=buildings,seed=1,dummyNodes=True) n = G.number_of_nodes() guardIdxs = list(np.random.choice(list(range(N+1,n-N-1)),k,replace=False))
visibleNodes = range(1,n-1) Gnodes = range(1,N+1) Rnodes = range(n-2,n-N-2,-1)
edgeVals = getGuardEffects(G,pos,guardIdxs,buildings=buildings,dummyNodes=[0,n-1]) edgeProbs = edgeVals.sum(axis=1) edgeProbs = np.exp(edgeProbs)
fig, ax = showPaths(G,pos,edgeProbs,visibleNodes=visibleNodes,Gnodes=Gnodes,Rnodes=Rnodes,guards=guardIdxs)
- for x,y,w,h in buildings:
rect = plt.Rectangle((x,y),w,h,fc=’y’,alpha=.3) ax.add_patch(rect)
解决示例
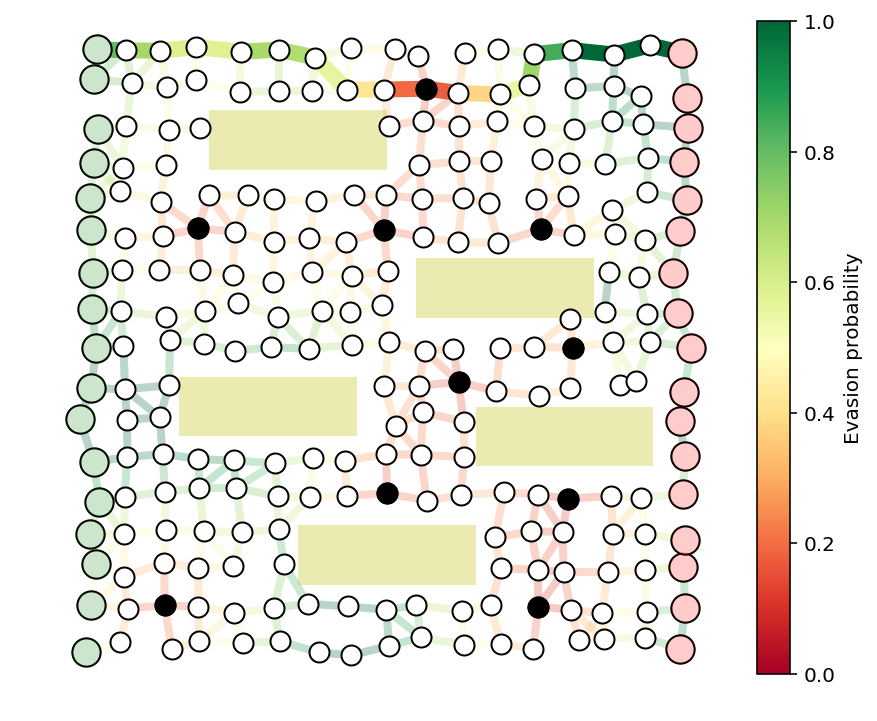
我们将解决一个带有建筑物、守卫和多个源和目的节点的更大的示例。我们将考虑在图的每个内部节点处放置一个守卫,并尽可能少地找出一定数量的守卫,例如10个,以尽可能保证图的安全性。
TODO
-优化形式 -结果显示,与上一结果不同,这是一个“真正”的整数规划问题; -使用迭代重新加权算法来获得布尔解; -使用松弛法对真实最佳解的距离进行限制
N = 17
buildings = [(.2,.8,.3,.1),
(.35,.1,.3,.1),
(.55,.55,.3,.1),
(.15,.35,.3,.1),
(.65,.3,.3,.1)]
G, pos = formGraph(N,.11,1.25,buildings=buildings,seed=0,dummyNodes=True)
n = G.number_of_nodes()
guardIdxs = list(range(N+1,n-N-1))
visibleNodes = range(1,n-1)
Gnodes = range(1,N+1)
Rnodes = range(n-2,n-N-2,-1)
edgeVals = getGuardEffects(G,pos,guardIdxs,buildings=buildings,dummyNodes=[0,n-1])
edgeProbs = edgeVals.sum(axis=1)
edgeProbs = np.exp(edgeProbs).. code:: python
fig, ax = showPaths(G,pos,edgeProbs,visibleNodes=visibleNodes,Gnodes=Gnodes,Rnodes=Rnodes,guards=guardIdxs)
fig.set_size_inches((16,8))
for x,y,w,h in buildings:
rect = plt.Rectangle((x,y),w,h,fc='y',alpha=.3)
ax.add_patch(rect)

A = nx.incidence_matrix(G,oriented=True).toarray()
n,m = A.shape
numGuards = len(guardIdxs)
b = np.zeros(n)
b[0] = -1
b[n-1] = 1
eps = 1e-1
w = np.ones(numGuards)
for i in range(2):
nu = cp.Variable(shape=n)
r = cp.Variable(shape=numGuards)
constr = [A.T*nu >= edgeVals*r, cp.sum(r) == 10, r >= 0, r <= 1]
cp.Problem(cp.Minimize(nu.T*b/100 + r.T*w),constr).solve(verbose=True)
nu = np.array(nu.value).flatten()
r = np.array(r.value).flatten()
w = 1/(eps+np.abs(r))
-----------------------------------------------------------------
OSQP v0.4.1 - 线性系统求解器
(c) Bartolomeo Stellato, Goran Banjac
牛津大学 - 斯坦福大学 2018
-----------------------------------------------------------------
问题: 变量 n = 448, 约束 m = 1305
nnz(P) + nnz(A) = 27688
设置: 线性系统求解器 = qdldl,
eps_abs = 1.0e-03, eps_rel = 1.0e-03,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (自适应),
sigma = 1.00e-06, alpha = 1.60, max_iter = 4000
检查终止: 开启 (间隔 25),
缩放: 开启, 缩放终止: 关闭
热启动: 开启, 优化: 开启
迭代 目标值 主次约束相对过程 对偶约束相对过程 rho 时间
1 -1.5225e-02 1.00e+01 1.24e+03 1.00e-01 1.50e-02s
200 9.8653e+00 5.33e-03 1.96e-03 1.98e-02 1.10e-01s
状态: 已解决
最优解优化: 不成功
迭代次数: 200
最优目标值: 9.8653
运行时间: 1.13e-01s
最优 rho 估计: 1.08e-02
-----------------------------------------------------------------
OSQP v0.4.1 - 线性系统求解器
(c) Bartolomeo Stellato, Goran Banjac
牛津大学 - 斯坦福大学 2018
-----------------------------------------------------------------
问题: 变量 n = 448, 约束 m = 1305
nnz(P) + nnz(A) = 27688
设置: 线性系统求解器 = qdldl,
eps_abs = 1.0e-03, eps_rel = 1.0e-03,
eps_prim_inf = 1.0e-04, eps_dual_inf = 1.0e-04,
rho = 1.00e-01 (自适应),
sigma = 1.00e-06, alpha = 1.60, max_iter = 4000
检查终止: 开启 (间隔 25),
缩放: 开启, 缩放终止: 关闭
热启动: 开启, 优化: 开启
迭代 目标值 主次约束相对过程 对偶约束相对过程 rho 时间
1 -5.7726e+02 1.00e+01 1.23e+04 1.00e-01 1.10e-02s
200 1.8639e+01 1.36e-02 4.08e-01 1.00e-01 5.95e-02s
400 1.9265e+01 2.46e-02 7.13e-02 1.92e-02 1.13e-01s
600 1.8962e+01 1.23e-02 5.74e-02 1.92e-02 1.61e-01s
800 1.8931e+01 7.97e-03 4.31e-02 1.92e-02 2.23e-01s
1000 1.8566e+01 6.39e-03 3.56e-02 1.92e-02 2.74e-01s
1200 1.8689e+01 8.31e-03 1.31e-02 1.92e-02 3.23e-01s
1225 1.8471e+01 7.94e-03 3.93e-03 1.92e-02 3.30e-01s
状态: 已解决
最优解优化: 不成功
迭代次数: 1225
最优目标值: 18.4712
运行时间: 3.31e-01s
最优 rho 估计: 2.86e-02
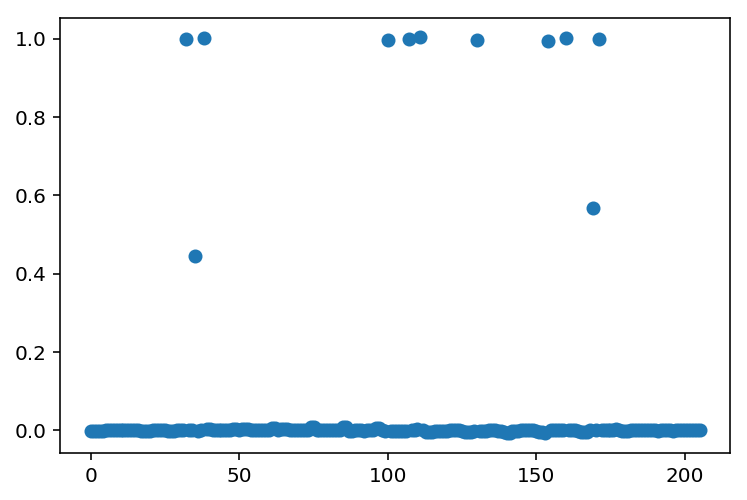
plt.plot(r,'o')
[<matplotlib.lines.Line2D at 0xd1b50d438>]
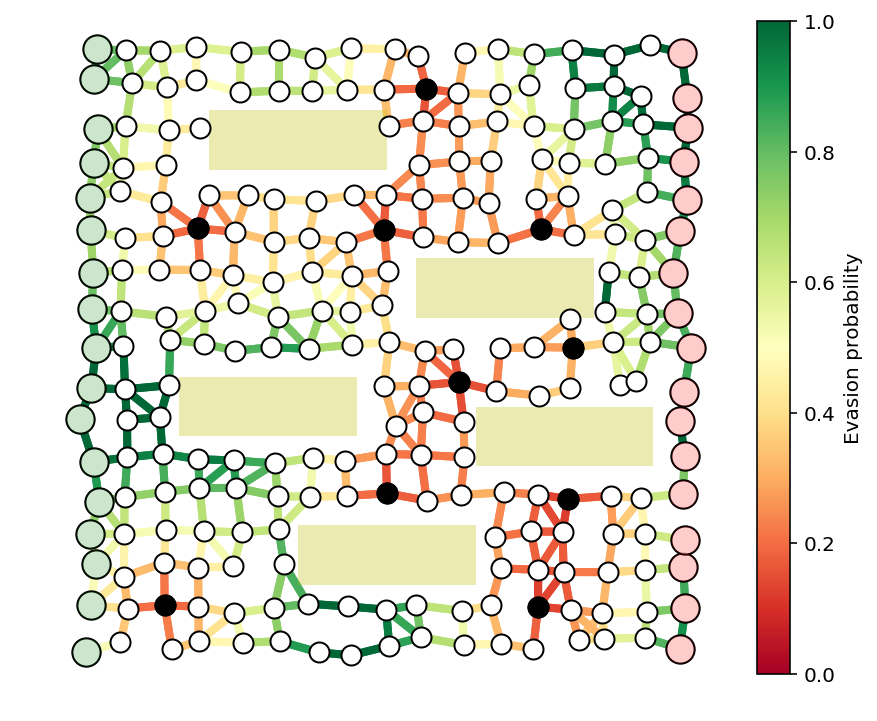
c = edgeVals.dot(r)
edgeProbs = np.exp(c)
guards = [guardIdxs[i] for i in range(len(guardIdxs)) if r[i] > .5]
fig, ax = showPaths(G,pos,edgeProbs,visibleNodes=visibleNodes,Gnodes=Gnodes,Rnodes=Rnodes,guards=guards)
for x,y,w,h in buildings:
rect = plt.Rectangle((x,y),w,h,fc='y',alpha=.3)
ax.add_patch(rect)
x = optPath(G,edgeProbs)
path_inds = list(np.flatnonzero(x > .1))
fig, ax = showPaths(G, pos, edgeProbs, path=path_inds, visibleNodes=visibleNodes, Gnodes=Gnodes, Rnodes=Rnodes, guards=guards)
print("走私者的最优路径的回避概率为 %e。" % (np.exp(x.dot(c)),))
for x, y, w, h in buildings:
rect = plt.Rectangle((x, y), w, h, fc='y', alpha=.3)
ax.add_patch(rect)
走私者的最优路径的回避概率为 9.213215e-05。