任意二维几何形状的阵列的波束宽度最小化
Judson Wilson于2014年5月14日创建的衍生作品。根据Almir Mutapcic于2006年2月2日的同名CVX示例进行了适应性修改(有重大改动)。
主题参考:
Boyd的“凸优化实例”讲义(EE364)
Lebret和S. Boyd的“通过凸优化进行天线阵列模式合成”
介绍
该算法设计了一个天线阵列,满足以下条件:
在某个目标方向上具有单位灵敏度
在波束外部满足最小旁瓣电平约束
最小化图案的波束宽度。
这是一个准凸问题。将目标方向定义为 \(\theta_{\mbox{tar}}\),波束宽度定义为 \(\Delta \theta_{\mbox{bw}}\)。波束占据角度区间
\[\Theta_b = \left(\theta_{\mbox{tar}}
-\frac{1}{2}\Delta \theta_{\mbox{bw}},\; \theta_{\mbox{tar}}
+ \frac{1}{2}\Delta \theta_{\mbox{bw}}\right).寻找最小波束宽度 :math:`\Delta \theta_{\mbox{bw}}` 的解通过二分法进行,\]
其中包含最优值的区间根据以下可行性问题的结果进行二分:
\[\begin{split}\begin{array}{ll}
\mbox{最小化} & 0 \\
\mbox{约束条件} & y(\theta_{\mbox{tar}}) = 1 \\
& \left|y(\theta)\right| \leq t_{\mbox{sb}}
\quad \forall \theta \notin \Theta_b.
\end{array}\end{split}\]
这里 \(y\) 是天线阵列增益图案(一个复值函数), \(t_{\mbox{sb}}\) 是最大允许旁瓣增益阈值, 而变量是 \(w\) (天线阵列权值或遮罩系数)。 增益图案是 \(w\) 的线性函数:\(y(\theta) = w^T a(\theta)\), 其中 \(a(\theta)\) 描述天线阵列的配置和规格。
一旦找到最优波束宽度,解 \(w\) 就通过以下优化进行细化:
\[\begin{split}\begin{array}{ll}
\mbox{最小化} & \|w\| \\
\mbox{约束条件} & y(\theta_{\mbox{tar}}) = 1 \\
& \left|y(\theta)\right| \leq t_{\mbox{sb}}
\quad \forall \theta \notin \Theta_b.
\end{array}\end{split}\]
下面的实现将角度数量及其对应的数量,如 \(\theta\),离散化。
问题规格和数据
天线阵列选择
选择其中一种:
随机的二维天线布局。
在一条线上均匀布局的一维天线。
在网格上均匀布局的二维天线。
import cvxpy as cp
import numpy as np
# 选择阵列几何形状:
ARRAY_GEOMETRY = '2D_RANDOM'
#ARRAY_GEOMETRY = '1D_UNIFORM_LINE'
#ARRAY_GEOMETRY = '2D_UNIFORM_LATTICE'
数据生成
#
# 问题规格。
#
lambda_wl = 1 # 波长
theta_tar = 60 # 目标方向
min_sidelobe = -20 # 最大旁瓣电平(单位:分贝)
max_half_beam = 50 # 起始半波束宽度(必须可行)
#
# 2D_RANDOM:
# 在二维中随机定位的n个天线元件。
#
if ARRAY_GEOMETRY == '2D_RANDOM':
# 设置随机种子以进行可重复实验。
np.random.seed(1)
# 在[0,L]×[0,L]的正方形上均匀分布。
n = 36
L = 5
loc = L*np.random.random((n,2))
#
# 1D_UNIFORM_LINE:
# 在一维上均匀分布的具有n个元件和元素间距d的阵列。
#
elif ARRAY_GEOMETRY == '1D_UNIFORM_LINE':
n = 30
d = 0.45*lambda_wl
loc = np.hstack(( d * np.array(range(0,n)).reshape(-1, 1), \
np.zeros((n,1)) ))
#
# 2D_UNIFORM_LATTICE:
# 具有m×m元素和距离d的二维均匀阵列。
#
elif ARRAY_GEOMETRY == '2D_UNIFORM_LATTICE':
m = 6
n = m**2
d = 0.45*lambda_wl
loc = np.zeros((n, 2))
for x in range(m):
for y in range(m):
loc[m*y+x,:] = [x,y]
loc = loc*d
else:
raise Exception('未定义的阵列几何形状')
#
# 构建优化数据。
#
# 构建将w和y(theta)(即y = A*w)关联的矩阵A。
theta = np.array(range(1, 360+1)).reshape(-1, 1)
A = np.kron(np.cos(np.pi*theta/180), loc[:, 0].T) \
+ np.kron(np.sin(np.pi*theta/180), loc[:, 1].T)
A = np.exp(2*np.pi*1j/lambda_wl*A)
# 目标约束矩阵。
ind_closest = np.argmin(np.abs(theta - theta_tar))
Atar = A[ind_closest,:]
使用二分算法求解
# 二分范围限制。每次减少一半。
halfbeam_bot = 1
halfbeam_top = max_half_beam
print('我们只考虑半波束宽度的整数值')
print('(因为我们以1度分辨率对角度进行采样)。')
print('')
# 二分迭代直到1度角度不确定性。
while halfbeam_top - halfbeam_bot > 1:
# 当前半波束的角度宽度。
halfbeam_cur = np.ceil( (halfbeam_top + halfbeam_bot)/2.0 )
# 创建停止带的优化矩阵,
# 即只有停止带角度的A值。
ind = np.nonzero(np.squeeze(np.array(np.logical_or( \
theta <= (theta_tar-halfbeam_cur), \
theta >= (theta_tar+halfbeam_cur) ))))
As = A[ind[0],:]
#
# 构造并解决可行性天线阵列问题。
#
# 在编写本文时(2014/05/14),cvxpy不能进行复数运算,
# 因此必须将实部和虚部分开存储并进行如下操作:
# 将任何向量或矩阵表示为a+bj,或A+Bj。
# 向量存储为[a; b],矩阵存储为[A -B; B A]:
# Atar为[A -B; B A]
Atar_R = Atar.real
Atar_I = Atar.imag
neg_Atar_I = -Atar_I
Atar_RI = np.block([[Atar_R, neg_Atar_I], [Atar_I, Atar_R]])
# As为[A -B; B A]
As_R = As.real
As_I = As.imag
neg_As_I = -As_I
As_RI = np.block([[As_R, neg_As_I], [As_I, As_R]])
As_RI_top = np.block([As_R, neg_As_I])
As_RI_bot = np.block([As_I, As_R])
# 1-向量为[1, 0](没有虚部)
realones_ri = np.array([1.0, 0.0])
# 创建cvxpy变量和约束条件
w_ri = cp.Variable(shape=(2*n))
constraints = [ Atar_RI*w_ri == realones_ri]
# 必须逐行逐行地手动添加复数约束
# abs(As*w <= 10**(min_sidelobe/20))。
# TODO:将来版本在cvxpy中实现复数数学或用norms()代替
# 当这些功能在cvxpy中可用时。
for i in range(As.shape[0]):
# 创建一个矩阵,其与w_ri的乘积是一2-向量,
# 其中第一行是As*w的实部,第二行是虚部。
As_ri_row = np.vstack((As_RI_top[i, :], As_RI_bot[i, :]))
constraints.append( \
cp.norm(As_ri_row*w_ri) <= 10**(min_sidelobe/20) )
# 构造并解决问题。
obj = cp.Minimize(0)
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.CVXOPT)
# 二分(或失败)。
if prob.status == cp.OPTIMAL:
print('当半波束宽度为{}度时,问题是可行的'.format(halfbeam_cur))
halfbeam_top = halfbeam_cur
elif prob.status == cp.INFEASIBLE:
print('当半波束宽度为{}度时,问题是不可行的'.format(halfbeam_cur))
halfbeam_bot = halfbeam_cur
else:
raise Exception('CVXPY错误')
# 最优波束宽度。
halfbeam = halfbeam_top
print('给定规格的最佳半波束宽度为{}'.format(halfbeam))
# 计算最佳波束宽度的最小噪声设计
ind = np.nonzero(np.squeeze(np.array(np.logical_or( \
theta <= (theta_tar-halfbeam), \
theta >= (theta_tar+halfbeam) ))))
As = A[ind[0],:]
# As为[A -B; B A]
# 参考之前的计算以获得实/虚表示
As_R = As.real
As_I = As.imag
neg_As_I = -As_I
As_RI = np.block([[As_R, neg_As_I], [As_I, As_R]])
As_RI_top = np.block([As_R, neg_As_I])
As_RI_bot = np.block([As_I, As_R])
constraints = [ Atar_RI*w_ri == realones_ri]
# 与上面相同的约束,但对新的As(因此实际上约束的数量不同)。
# 请参阅上面的注释。
for i in range(As.shape[0]):
As_ri_row = np.vstack((As_RI_top[i, :], As_RI_bot[i, :]))
constraints.append( \
cp.norm(As_ri_row*w_ri) <= 10**(min_sidelobe/20) )
# 构造并解决问题。
# 注意新的目标!
obj = cp.Minimize(cp.norm(w_ri))
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.SCS)
#if prob.status != cp.OPTIMAL:
# raise Exception('CVXPY Error')
print("final objective value: {}".format(obj.value))
我们只考虑半功率束宽的整数值
(因为我们以1度的分辨率对角度进行采样)。
半功率束宽为 26.0 度时问题可行
半功率束宽为 14.0 度时问题可行
半功率束宽为 8.0 度时问题不可行
半功率束宽为 11.0 度时问题可行
半功率束宽为 10.0 度时问题可行
半功率束宽为 9.0 度时问题可行
给定规格的最佳半功率束宽为 9.0
最终目标值: 1.6616084212553195
结果图表
import matplotlib.pyplot as plt
# 在 ipython 中内联显示图表。
%matplotlib inline
# 图表属性配置。
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
#
# 第一张图:天线位置
#
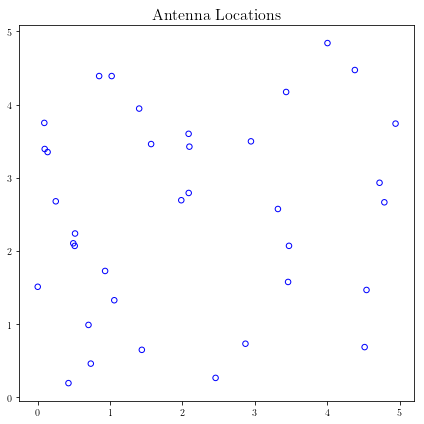
plt.figure(figsize=(6, 6))
plt.scatter(loc[:, 0], loc[:, 1],
s=30, facecolors='none', edgecolors='b')
plt.title('天线位置', fontsize=16)
plt.tight_layout()
plt.show()
#
# 第二张图:阵列图案
#
# 复数数学计算 y = A*w_im;
# 有关使用实部表示复数的详细注释,请参见上述代码。
A_R = A.real
A_I = A.imag
neg_A_I = -A_I
A_RI = np.block([[A_R, neg_A_I], [A_I, A_R]]);
y = A_RI.dot(w_ri.value)
y = y[0:int(y.shape[0]/2)] + 1j*y[int(y.shape[0]/2):] # 现在是本地复数
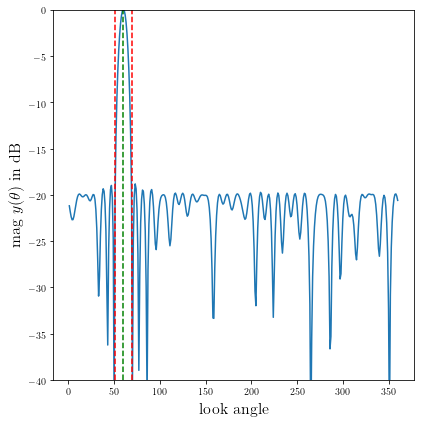
plt.figure(figsize=(6,6))
ymin, ymax = -40, 0
plt.plot(np.arange(360)+1, np.array(20*np.log10(np.abs(y))))
plt.plot([theta_tar, theta_tar], [ymin, ymax], 'g--')
plt.plot([theta_tar+halfbeam, theta_tar+halfbeam], [ymin, ymax], 'r--')
plt.plot([theta_tar-halfbeam, theta_tar-halfbeam], [ymin, ymax], 'r--')
plt.xlabel('视角', fontsize=16)
plt.ylabel(r'mag $y(\theta)$(单位:分贝)', fontsize=16)
plt.ylim(ymin, ymax)
plt.tight_layout()
plt.show()
#
# 第三张图:极坐标图案
#
plt.figure(figsize=(6,6))
zerodB = 50
dBY = 20*np.log10(np.abs(y)) + zerodB
plt.plot(dBY * np.cos(np.pi*theta.flatten()/180),
dBY * np.sin(np.pi*theta.flatten()/180))
plt.xlim(-zerodB, zerodB)
plt.ylim(-zerodB, zerodB)
plt.axis('off')
# 0 dB 级别。
plt.plot(zerodB*np.cos(np.pi*theta.flatten()/180),
zerodB*np.sin(np.pi*theta.flatten()/180), 'k:')
plt.text(-zerodB,0,'0 dB', fontsize=16)
# 最小旁瓣级别。
m=min_sidelobe + zerodB
plt.plot(m*np.cos(np.pi*theta.flatten()/180),
m*np.sin(np.pi*theta.flatten()/180), 'k:')
plt.text(-m,0,'{:.1f} dB'.format(min_sidelobe), fontsize=16)
#Lobe 中心和边界角度。
theta_1 = theta_tar+halfbeam
theta_2 = theta_tar-halfbeam
plt.plot([0, 55*np.cos(theta_tar*np.pi/180)], \
[0, 55*np.sin(theta_tar*np.pi/180)], 'k:')
plt.plot([0, 55*np.cos(theta_1*np.pi/180)], \
[0, 55*np.sin(theta_1*np.pi/180)], 'k:')
plt.plot([0, 55*np.cos(theta_2*np.pi/180)], \
[0, 55*np.sin(theta_2*np.pi/180)], 'k:')
# 显示图表。
plt.tight_layout()
plt.show()